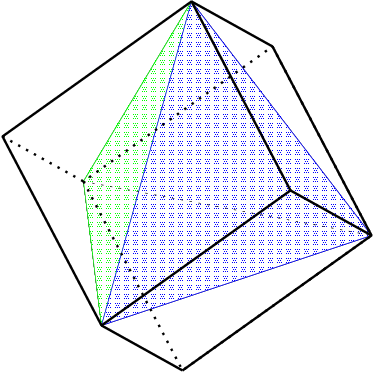
立方体と四面体の関係
講義の題は「形と影」です.さまざまな立体の影の形を考えては,プロジェク タを使って実際に影を作りそれを検証していきます.結果を見て楽しむのでは なく,とにかく考えさせ,その中で自然に数学的帰納法の考え方を身につける のが目的です.
球(ボール): どんな影になりますか?
もちろん,円です.
正四面体: どんな影になりますか?
ボールの影を見せた後だからでしょう,たいていの生徒が三角形と答えてくれ
ました.もちろん,光を当てる方向によって影の形は変わります.そしてそれ
は,4つの正三角形の面の影を合わせた形です.正三角形の影は,3つの頂点
の影の3点を結んでできる三角形か線分です.ですから,正四面体の影は,4つ
の頂点の影の4点から3点を選んで結んでできる4つの図形の和であり,4点が
一直線上に並ぶことはないので,三角形か四角形です.[もちろん,このように
説明したのでは,小学生はついてこれません.立体をいろんな方向から見せ
ながら,輪郭の形がどのように変化するか観察させるのがいいでしょう.]
正四面体(辺の方向から投影): では,光を当てる方向を, 辺の中点から相対する辺の中点にぬける方向にした時にはどんな影になるでしょうか.
正四面体のその辺を鉛直にして この方向から見ると, 左右対称,上下対称です.ですから,その影も,左右対称,上下対称のはずで, ひし形だとわかります.さらに,対角線の長さも等しいので,正方形です. [もちろん,プロジェクタは点光源なので,実際にはひし形にしかならないのですが,平行光線と仮定して話をすすめました.]

正方形の影ができることは,立方体と正四面体の関係を考えると分かりやすい です.上図のように,立方体から4つの頂点を切り落とすと正四面体ができま す.正四面体を立方体に入れて考えると,辺の方から正四面体を見るというの は,立方体の面の方から見ることになり,正方形に見えているのです.このこ とから,正四面体が正方形に見える方向,すなわち,向かい合う辺の中点を結 ぶ直線は3本ありますが,それらは互いに直交していることが分かります.
用意した立方体の模型は,このことを説明するために,上図のように分解して 中から正四面体を取り出せるようにしておきました.正四面体が正方形に見え ることは,物事は見る方向を変えれば見え方が違ってくると示唆的ですし,正 多面体どうしの関係から説明できるのも奥深く,小学生に話したかったことの 一つです.
1-シェルピンスキー四面体(辺の方向から投影): ここからが重要 です.正四面体の模型も細工をして,真ん中の正八面体を取り出して,1-シェ ルピンスキー四面体にできるようにしておきました.1-シェルピンスキー四面 体に辺の方から光を当てたときの影の形はどうなるでしょう?
全体が正四面体に穴をあけた形なので,その影も,正方形に穴をあけた形のは ずです.また,1-シェルピンスキー四面体をなす,4つの正四面体がそれぞれ 1/2の大きさの正方形の影を作るはずです,そして,それら4つの正方形は,頂 点で互いにつながっているはずです,これらのことから,穴がふさがって,正 方形になると推論することができます.
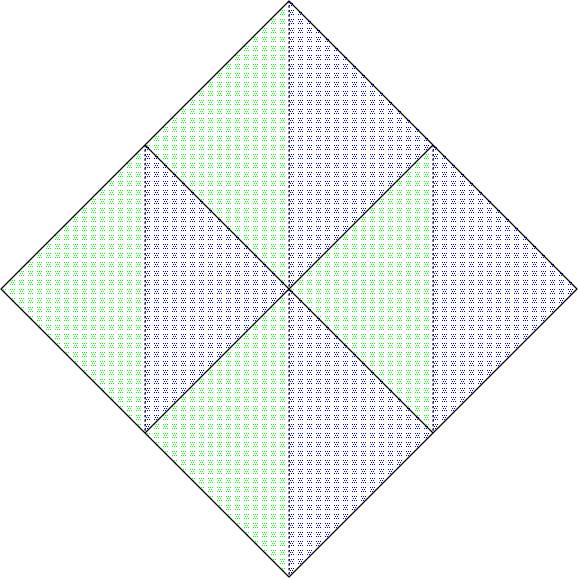
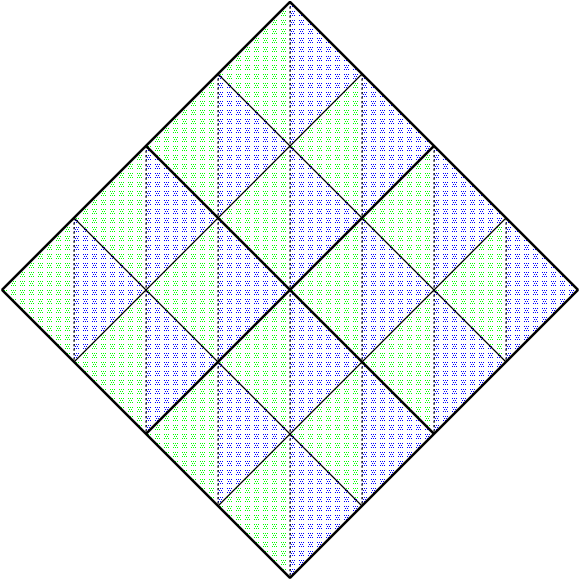
模型を用意したのはここまでです.ここで,3-シェルピンスキー四面体のそれ ぞれの正四面体に穴をあけて4-シェルピンスキー四面体にしたときにはどうな るか,これをさらに繰り返して,どんどん細かくしていったときにどうなるか, 考えてもらいました.同様に考えて,どこまで続けても正方形になることが理 解してもらえれば,この授業は成功です.
言うまでもなく,これは,数学的帰納法です.数学的帰納法は,有限の推論か ら「どんな n に対しても…」という無限個の場合で成り立つ法則を導く,大 切なものです.現在,数学的帰納法は,漸化式と一緒に高校2年で習うことになっ てますが,その感覚を自然に体感してもらえたのではないかと思っ ています.
これで,中学生にはちょうどいい難易度だったと思います.小学校で行った講 義では,正四面体はもちろん三角柱も教科書には載っていないのですから,生 徒も私も苦労しました.一回だけの授業ではなく何回も時間をかけて行えれ ば,「小学生から帰納法」も不可能ではないと思うのですが,いかがでしょう か.その分,次号で紹介する工作は,十分楽しんでもらえました.
このように,シェルピンスキー四面体は極限操作で定義されてい るので,その性質の証明には,どうしても位相的な議論が入ってきます.それ は,有限再帰図形が数学的帰納法で考えられる世界であるのと対照的です.こ のように,両者は,数学的にも計算機科学的にもまったく扱いが異なります. 有限再帰図形と自己相似図形の関係は,有理区間と実数の関係と同じといって いいでしょう.パソコンに絵を描かせてフラクタルに対するイメージを湧かせ るのは重要です.しかし,パソコンが瞬時に細かいところまで描画してくれる のを見ると,無限の極限を手に入れたかの錯覚を覚えるのではないかと思いま す.時には,パソコンなど用いずに,有限のものを手で描いたり,あるいは工 作したりしながら,その無限の極限について想像することも数学教育には重要 だと思うのですが,いかがでしょうか.