- この立体は何ですか？
４次元立体である切頂１２０胞体を３次元に射影したものです。本当は球形をしていますが、その、半分よりちょっと大きい部分を，総合人間学部／人間・環境学研究科の授業で制作しました。
- ４次元って何ですか？
直交する座標軸を２つとれれば２次元、３つとれれば３次元ですね。４つとれる空間を４次元空間といいます。物理では、４つ目の座標軸として時間をとった４次元時空を考えますが、ここでは、４つとも対等な空間（ユークリッド空間と呼ばれています）を考えています。
- ４次元空間は存在するのですか？
数学的に定義できるという意味では存在しています。この３次元空間の中にそのようなものが体感できる形であるかといえば、ないでしょう。
- 切頂１２０胞体について教えてください。
３次元空間に正１２面体などの正多面体があります。
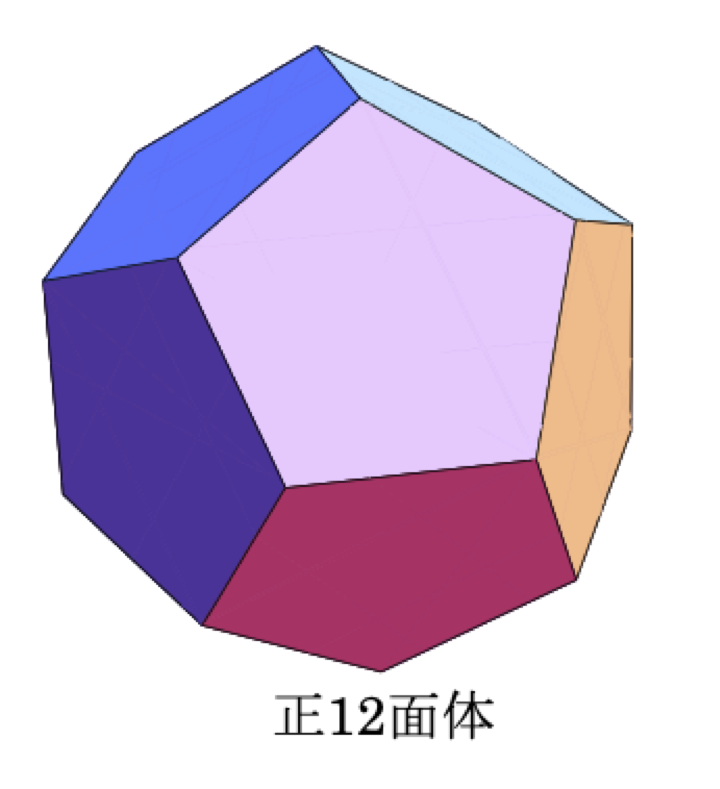それと同様に、４次元空間に、正１２０胞体などの正多胞体があります。正１２面体が、１２個の正５角形の面に囲まれているように、正１２０胞体は、１２０個の正１２面体に囲まれています。正12面体は，頂点の周りを３つの正五角形が囲んでいます。よって，正１２面体の頂点の周りを切ると，正3角形ができます。このようにして，２０個全ての頂点の周りを切ると、正１０角形１２個と正３角形２０個に囲まれた立体（切頂１２面体）ができます。
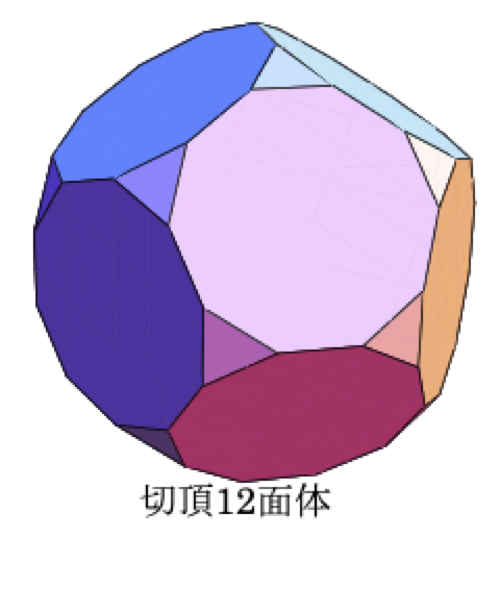同じように、正１２０胞体の各頂点の周りには，４個の正12面体が集まっています。そして，その頂点の周りを切ると１２面体１２０個と正４面体６００個からなる立体（切頂１２０胞体）ができます。
- 射影とは何ですか？
写真をとると、３次元のものが２次元の紙上に表されます。これは、(x,y,z) という３次元座標の z の値を忘れて (x,y) という２次元座標の点を考えることに対応します。これを射影といいます。この立体も，切頂１２０胞体を，胞（切頂正12面体）が w軸方向に来るように配置して，4 次元から3次元へ射影，すなわち，(x,y,z,w) という4次元座標に対して，w の値を忘れて (x,y,z) という3次元座標をとるようにして3次元空間上で表現してできた図形です。
2次元の写真から3 次元立体を想像するように，このオブジェから， 切頂120 胞体が 4 次元のどんな立体か想像してみましょう。
- この立体は，何を使って作ってあるのですか
Ｚｏｍｅツールという，数学模型を作る道具を用いて作成しています。
頂点のボールは，正１２面体の頂点方向に５角形の穴，正20面体の頂点方向に三角形の穴，それらの辺方向（３０個あります）に長方形の穴があいています。それらに，赤色（５角形），
黄色（３角形），青色（長方形）の棒を挿して，立体を作ります。棒は，それぞれの色で黄金比をなすような長さの比のものが用意されています。この立体は，赤は長と中の２つの長さ，青と黄色は一つの長さの棒だけを用いています。
- この立体は誰が考えたのですか？
切頂１２０胞体自体は，数学的に定義されたもので，誰が考え出したというのは難しいです。この部分だけを切り出すと，この大きさのＺＯＭＥツールで人間が中に入ることにより物理的に組み立てられられることに気がついて，このオブジェのデザインをしたのは塚本靖之氏（2016年3月人間・環境学学位取得）です。これまでに，京都大学総合博物館の夏休み子供教室や学祭の研究室企画で同じものを作ってきました。
塚本靖之氏(2015)
2017 年度の製作
- 中に入ると、ご利益がありますか？
形がよく分かります。そして，数学が好きになると思います。
- 私も中に入ってみたいです。
中に入れるイベントを行いますので，近くの掲示をみてください。勝手に入ったり，触ったりしないでください。このＺＯＭＥツールはかなり劣化していますので，すぐ折れます。
- 私も作ってみたいです。
メールを頂ければ，次の製作の機会に連絡します。
- これを見て四次元が分かりますか？
射影から元の４次元図形をある程度想像できます。例えば、写真に撮っても５角形は５角形ですよね。ただ、もともと正５角形であっても、斜めから写真をとると、ひしゃげた５角形になるし、真横からとると完全につぶれて線分になります。
この立体をよく見てください。切頂１２面体や正４面体のひしゃげたものがたくさん含まれています。完全につぶれて、平面図形になったものもあります。でも，4次元では，全てきれいな切頂１２面体や正４面体です。
- もっと教えて下さい。
もちろんです。順を追って説明していきましょう。
- 3次元から2次元への射影について
射影によってどのように図形がひしゃげるかが分かれば，射影から元の図形を想像する手助けになります。まず，3次元から2次元への射影を考えましょう。
正12 面体を，いろんな方向から射影した絵を考えましょう。
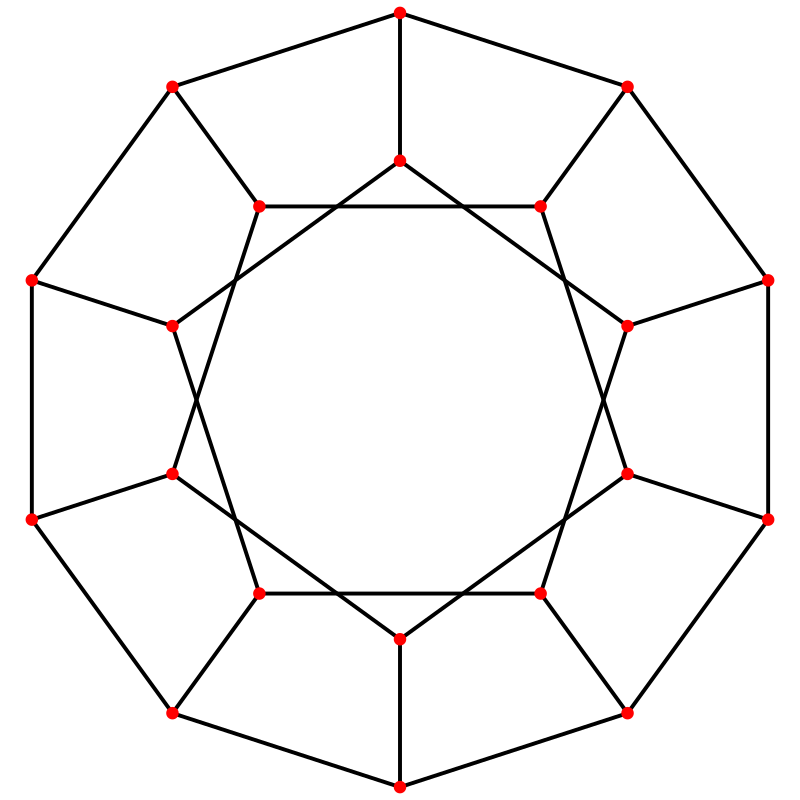
正12面体の面からの射影
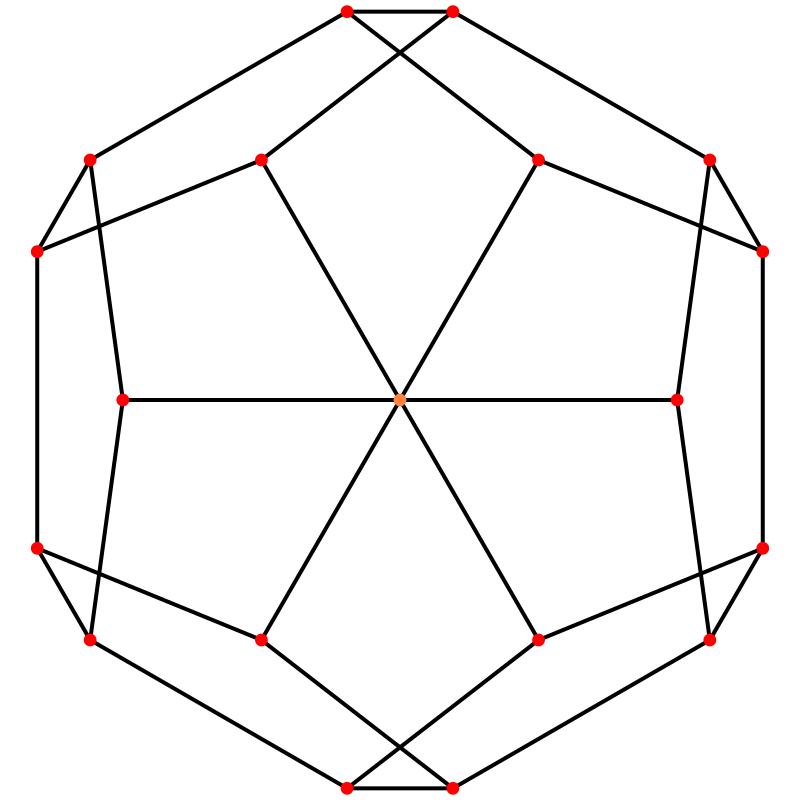
正12面体の頂点からの射影
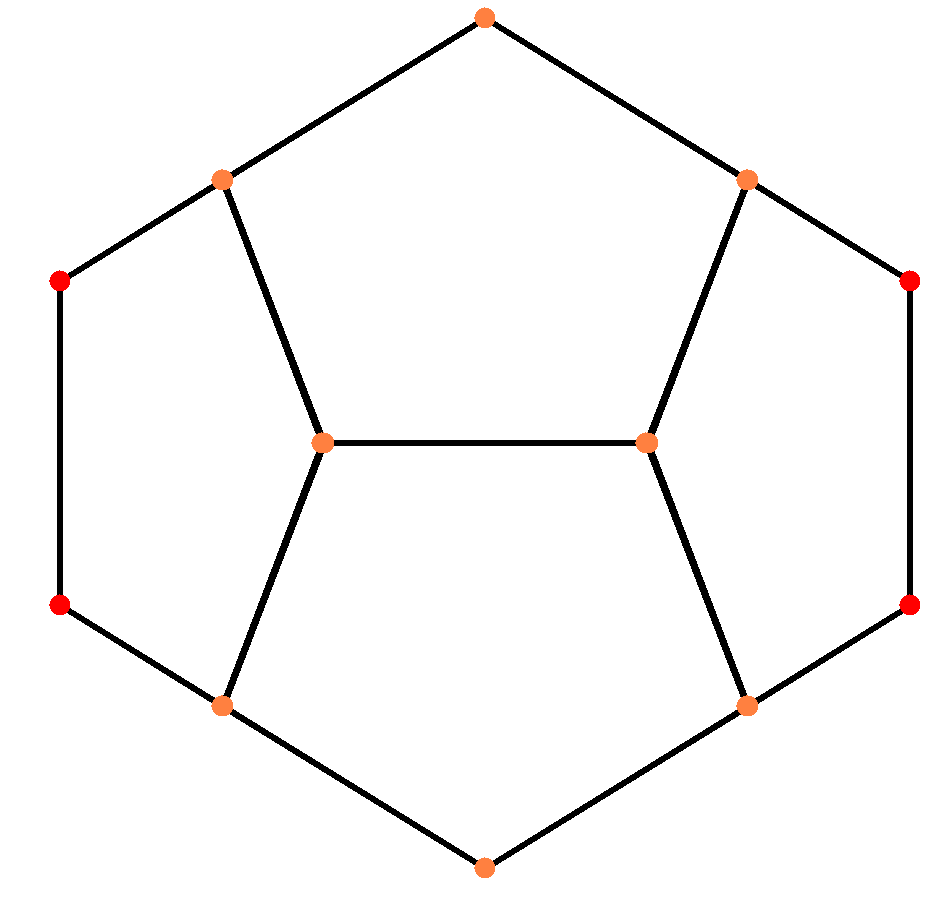
正12面体の辺からの射影
(Wikipedia より)
頭の中で，正12面体を少しだけ回しながら考えてください。
面と頂点からの射影では，手前の辺と奥の辺が重なってかかれていますが，分かりますか？
辺の方向から射影した時には，手前の辺と奥の辺ぴったり重なって，こんな綺麗な形になります。正12面体は立体図形ですが，全ての頂点が球面上にのっていて中は空洞なので，平面図形に近い立体図形です。実際，射影しても，高々，手前と奥の2重にしか重なりません。
表面の形状だけを考えればいいのですから，中のつまった立体図形を考えるのよりずっと簡単です。
これらの図から感じて欲しいのは，射影すると3次元のものを2次元に押し込むためにゆがみが生じてますが，つながり方は変わらないということです。
射影でも，5角形は5角形ですし，どの頂点も３つの辺がつながっています。
ただし，そのゆがみは，真ん中のあたりは少なくて，端にいくほど，ゆがみが強くなっていきます。そして，
辺からの射影では，周りの4枚の正5角形が線分までひしゃげてしまっています。また
周りの６つの頂点では，奥行き方向に辺が出ていて見えなかったり，手前側と奥側の中間に頂点があって，そこから出ている手前と奥の辺が重なって１つに見えたりして，２つしか辺が出てないように見えています。このように，周辺ではひしゃげすぎて例外的なことが起こりますが，あまりゆがみのない真ん中のあたりでは，ほぼ，3次元空間での配置と同じように見えています。 ここでは面の形が正5角形なので分かりにくいですが，
つながり方が同じだけではなく，並行なものは並行になるし，後で丁寧に説明するように，それぞれの面は，ある1方向に一定の比率でひしゃげた形になっています。
- この立体の見方
120胞体の3次元射影でも同じです。120胞体は４次元図形とはいえ，3次元図形が四次元的に少しづつ向きを変えながら，表面でつながっている形です。射影しても，手前側と奥側しか重なりません。しかも，
ここでは表面に12面体がある方向から射影していますが，この方向からの
射影では，正12面体の辺からの射影の時と同じ様に
手前側と奥側がぴったり重なります。ですので，この3次元立体を見ると，4次元空間内での切頂12面体と正4面体のつながり方が見てとれます。
特に，真ん中に近いところでは，ゆがみが少なく4次元の状況が分かりやすいです。
真ん中に，青い辺のみからなる大きな切頂１２面体があるのが分かりますか？
実は，この射影は，表面に切頂12面体が存在する方向から射影しています。ですので，射影の中心には切頂12面体が来ます。この点は，正12面体の面からの射影とよく似てます。
この，オブジェの中心にある切頂12面体を A と呼ぶことにします。
その周りを見ると，三角形の面の外側に次のような四面体がついています。
これは，ほとんど正四面体ですが，赤い辺の方が青い辺より短いので，少し背が低くなっています。それから，真ん中の切頂１２面体と正10角形の面を接するように，少しゆがんだ切頂１２面体があるのが分かりますか？これらの切頂１２面体の形を B と呼ぶことにします。
この，B の切頂１２面体は，切頂１２面体の(正10角形の)面方向にあるので，オブジェの下の方の作られていない部分も含めると12 個あります。
それら３つと真ん中の切頂１２面体 A とで，四面体をとりかこんでいます。
これは，4次元では，完全な切頂１２面体 4 つと正4面体のはずです。
- 120胞体と切頂120胞体
120胞体は，各頂点で4つの正12面体がつながっています。
これは，正12面体の頂点で，どのように3枚の正 5 角形がつながっているかのアナロジーで考えると分かりやすいです。
2次元平面の中では，3枚の正 5 角形を互いにつなげようとしても，すきまができてしまい不可能です。しかし，真ん中の頂点を3次元方向にはみ出させれば，つなげることができます。
正 120 胞体の頂点も同じです。3次元空間でも，１点のまわりに4つの正12面体の頂点を集めることができます。しかし，それらの間にはすきまがあります。その隙間をなくすことは3次元空間内では無理ですが，もう一つ次元をあげて，4次元空間空間内で正12面体を回転させて，真ん中の頂点の w 座標を正にすることにより，４つの正12面体をくっつけることができます。
雑な言い方ですが，これを繰り返すことにより正 120 胞体はできています。
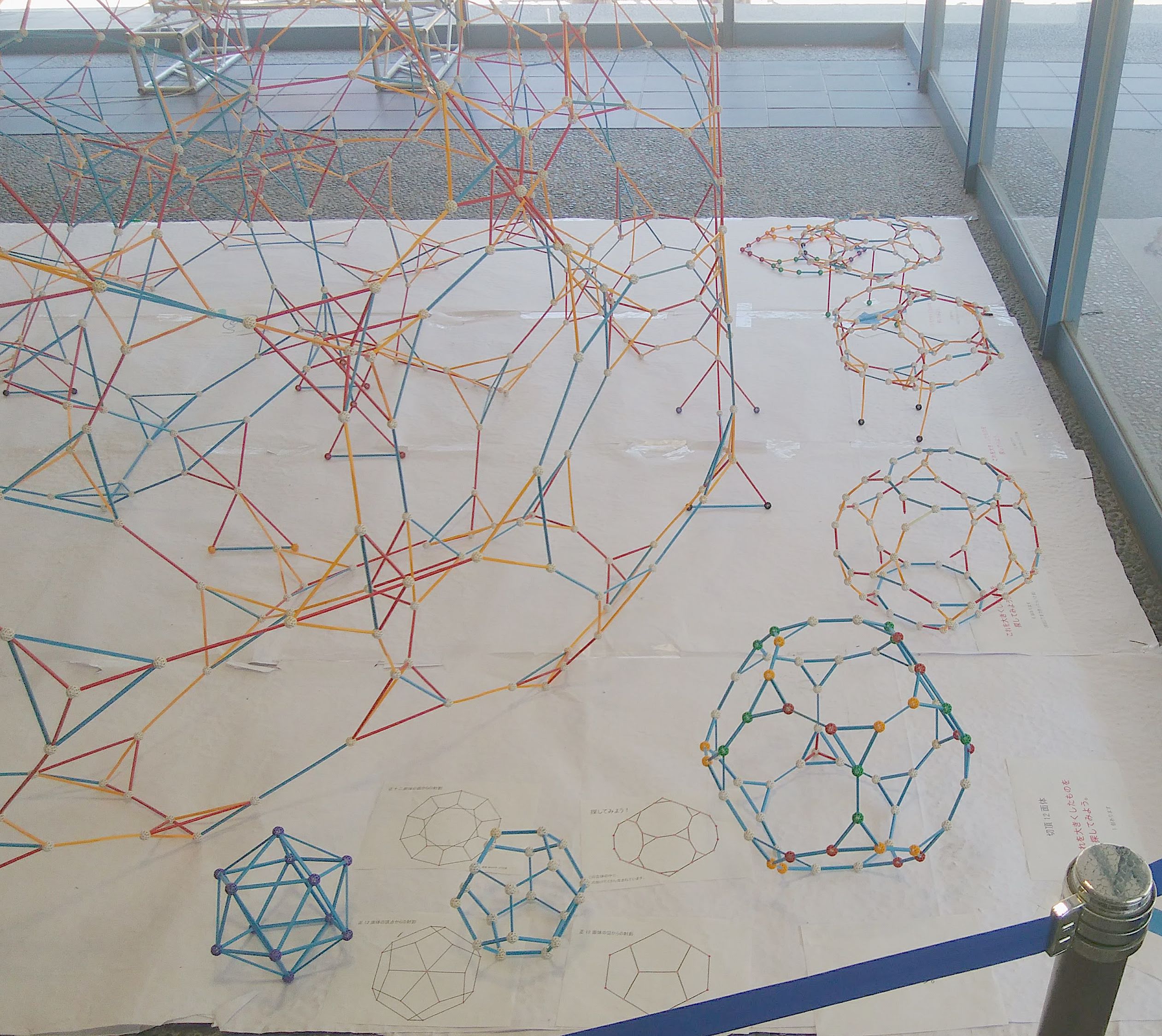
大きなドームの横に，正120 胞体の３次元射影があります。こちらの方は，上半分ではなくて，全体を作っています。その真中に，青い棒で作られた正１２面体があるのが分かりますか？これは，切頂１２面体の A に対応しています。そして，そのそれぞれの面の外側にも１２面体があります。これらは B に対応します。そしてそれらは，お互いに面でくっついていて，それぞれの頂点の周りに４つの１２面体が，頂点を共有して存在します。４次元では，これら全てが正１２面体なのですが，３次元に射影しているので，周りのものがゆがんで見えています。この説明は４次元ドームオブジェをベースに書いていますが，必要に応じて，より単純な正120 胞体の方を見て考えてください。
さて，そうやってできた立体の頂点の周りを切ることを考えましょう。正12面体の頂点は，平面で切ることができました。すると，その切口に正3角形ができて，切頂12面体ができました。今度は，120胞体の頂点の周りを3次元空間で切ることを考えます。すると，切口には正四面体ができます。
２つの立体を見比べながら考えてください。
正12面体から切頂正12面体を作る時の類推で，だいたいの雰囲気はイメージできたのではないでしょうか。ただし，ここまでの説明は直感的なものです。4次元の立体は，数式を用いて数学的に定義されたものなので，それがどうなっているかを，数式や数学的概念を用いずに正確に理解することは不可能です。興味を持った人は，数学的により厳密な定義のもとで，考えてみてください。
- さらに外側に
目をもう少し外側に向けると，たくさんのゆがんだ切頂１２面体と四面体が見えてきます。
まず，先ほどの Bの切頂１２面体の外側に，もっとゆがんだ切頂１２面体 C があります。
Cも，このオブジェの下の方の作られていない部分も含めると12 個あります。
さらに，B や C と10角形の面を共有して，ゆがんだ切頂１２面体 D があります。
D は，真ん中のA の切頂１２面体の，(正１２面体における) 頂点方向にあるので，下の方までオブジェを作れば 20 個あるはずです。
B や C は，切頂１２面体の(10角形の)面方向に縮小されていました。
それに対して，D は，(正１２面体における) 頂点方向に縮小されていましす。
さらに外側を見ましょう，このオブジェの表面に，もっとゆがんで，平面状になってしまった切頂１２面体 E があります。
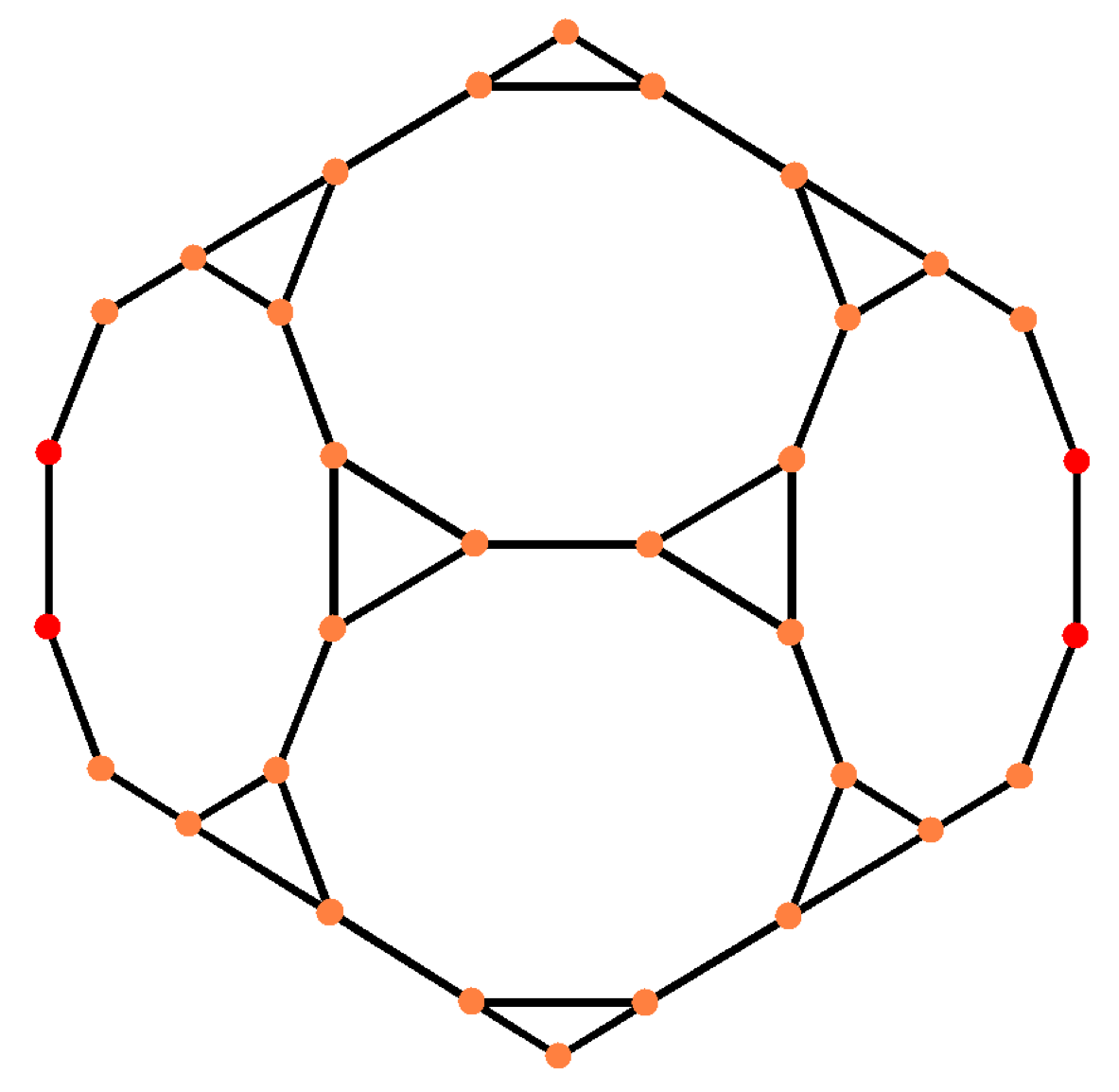
切頂12面体の辺からの射影(Wikipedia より)
下の切頂１２面体の絵を頭の中で少しだけ回転させれば，
これが切頂１２面体の辺の方向からの射影になっていることが分かると思います。
E は，真ん中の切頂12面体の辺方向にあるので，このオブジェを下の方まで作れば，全体で 30 個含まれるはずです。
A から E の立体は，短い Zome ツールを用いて作ったものが展示されています。
これを，このオブジェの中から探してみてください。
- 座標について
写真を見てもとの３次元の風景を想像できるのは，忘れられた z 座標を人間の脳が補うからです。普通の人間は自動的に4次元目のw座標を補うことができません。しかし，この立体の場合には，考えながら補うことができます。この立体の全ての頂点は，４次元空間で，切頂 120 胞体の中心となる点から等距離（1とします）にあります。つまり，x2+y2+z2+w2 = 1 です。そのことから，各頂点のw 座標は，射影の中心からの距離 d を元に √(1 - d 2)と簡単に分かります。
まず，真ん中には頂点はありませんが，もしあったとすると，(x, y, z)=(0,0,0) なので，w 座標は 1 と -1 です。真ん中の切頂１２面体 A の頂点は，
このオブジェの中心から同じ距離の所にあるので，4次元空間で同じw 座標の値 k を持ちます。4次元空間で，１つ次元の低い3次元空間のことを超平面といいます。少し難しい言い方をすれば，xyz-座標軸のはる超平面 (w=0)と，この切頂１２面体が存在する超平面 (w=k)は平行です。 (k の値は，± (3 + √5)/(4√2) = 0.9256... です。)
このオブジェの中で，青い辺は，w 軸と垂直な辺です。青い辺でつながった 2 つの頂点は，w 座標が同じです。このオブジェは，4種類の長さの辺からでできていました。4次元では全て同じ長さの辺なので，同じ種類の辺は，w 軸となす角度が同じです。このように見ていくと，このオブジェから(切頂)120胞体の構造が分かってきます。
- 個数について
このように，この立体の中には，（ゆがんだ）切頂12面体が，A は 1 個，B と C の形はそれぞれ 12 個，D は 20個，
E は 30 個ふくまれています。A, B, C, D は，w 座標が正の部分と負の部分のものが重なって現れているので，実際にはこの2倍
の個数があります。また，E は，ちょうど，w = 0 をまたぐ形で存在しており，2重にはなりません。このことは，
正一二面体の辺方向への射影の周辺部と同じ状況です。
ですので，合わせると，4次元空間には，(2 + 12 + 12 + 20) x 2 + 30 = 120 個の切頂一二面体があることになります。
- 射影の形について
なぜ B, C, D, E のような縮小のされ方をした立体が切頂120胞体の射影の中に含まれるのかは，ベクトルを用いて説明すると分かりやすいです。
4次元から3次元への射影も3次元から2次元への射影も理屈は同じなので，3次元から2次元の場合で考えましょう。
3次元空間から z 座標に並行に， xy-平面への射影を考えます。3 次元空間内に，平面図形 A が存在したとして，A を xy-平面に射影した図形 B と A との関係が知りたい訳です。 A を含む平面をαとおきます。α と xy-平面の交線を P とし，P 方向の単位ベクトル p と，それに直交するα上の単位ベクトルを q をとって，α上に p と q からなる座標系を入れて考えます。この xy-平面への射影で，p は
射影方向と直交しているので長さが変わりません。よって，q 方向だけが，射影によって縮小されることになります。このようにして，B は A をある方向に縮小した図形になります。
4 次元から 3 次元の時には，P が2次元空間になるだけで，後は同じです。その時，P ，すなわち射影先の3次元空間と射影される12-20面体を含む3次元空間の共通部分に並行な辺は，青色をしています。
- 本当なんですか？
この説明は，納得してもらえましたか？私の気持ちとしては，簡単に納得してもらいたくないです。もっと根源的な，次のような質問に私は答えていません。
- 4次元空間に 120 胞体なる立体が存在するのは本当ですか？
Wikipedia や本を見るとそう書いてありますが，本当でしょうか。座標を用いて計算で示すのは可能ですが，それ以外に方法はあるでしょうか？
- このこの目の前のオブジェがその3次元射影の一部というのは本当ですか？
Zome ツールという，とても制限された方向に制限された長さの辺を作ることしかできない道具で，本当に正 120 胞体や切頂 120 胞体の3次元射影ができるのでしょうか。目の錯覚に（あるいは私に）ごまかされていないという保証はありますか？
- なんでこんなにうまくできるのですか？
これが間違いなくそういうオブジェであることは，座標を用いて確認できるでしょうが，なぜこんなにうまくできるのでしょうか？ Zome ツールの仕組みの中に，3 次元，4 次元の幾何と関係したきれいな数学的な構造が潜んでいそうですね。
ゆっくりと時間をかけて勉強をして，こういった疑問を解消してください。
- もっといろんな方向に射影した形を見たいんですけど...
正１２０胞体やそれの切頂体の座標はきれいな数なので，この形は，比較的容易にプログラムを組んで，コンピュータで可視化することができます。ゾムで作れるのは胞の方向からの射影だけなので，４次元的に回転すると，違った像が見えてきます。今はやりのVRゴーグルはコンピュータで３次元を扱うことを可能にしましたが，人類は，それを使って４次元で遊べるようになるのでしょうか。
人間・環境学研究科，数理科学講座，数理情報論分野
立木秀樹
参考文献：
- 『正多面体を解く』 一松信著， 東海大学出版会, 2002年
- 『高次元の正多面体』 一松信著， 日本評論社, 1983年
- 『目で見る高次元の世界』 トーマス・F・バンチョフ著，永田雅宜，橋爪道彦訳， 東京化学同人 1994年
- 『高次元図形サイエンス』 宮崎興二編
