グレイコードと実数
立木秀樹
共立出版 bit 2000年 1 月号
| 数 | 2進コード | グレイコード |
| 0 | 0 0 0 0 | 0 0 0 0 |
| 1 | 0 0 0 1 | 0 0 0 1 |
| 2 | 0 0 1 0 | 0 0 1 1 |
| 3 | 0 0 1 1 | 0 0 1 0 |
| 4 | 0 1 0 0 | 0 1 1 0 |
| 5 | 0 1 0 1 | 0 1 1 1 |
| 6 | 0 1 1 0 | 0 1 0 1 |
| 7 | 0 1 1 1 | 0 1 0 0 |
| 8 | 1 0 0 0 | 1 1 0 0 |
| 9 | 1 0 0 1 | 1 1 0 1 |
| 10 | 1 0 1 0 | 1 1 1 1 |
| 11 | 1 0 1 1 | 1 1 1 0 |
| 12 | 1 1 0 0 | 1 0 1 0 |
| 13 | 1 1 0 1 | 1 0 1 1 |
| 14 | 1 1 1 0 | 1 0 0 1 |
| 15 | 1 1 1 1 | 1 0 0 0 |
自然数が計算機の中で 2 進法により表現さ
れていることは、みなさんご存じだろう。し
かし、それ以外にも自然数の '0' と '1' の
列としての表現で有用なものが存在する。こ
のコードは、グレイコードと呼ばれている。
2 進法は 0, 1, 10, 11 と始まる
がグレイコードは、0, 1, 11, 10 と始まる。
一般に、2 進法では n 桁のコードを生成す
るのに n 桁目を 1 にしてそこまでのコード
を繰り返してたのに対し、グレイコードでは、
n 桁目を 1 にしてそこまでのコードを逆の
順番に用いている。つまり、新しい桁を 1
にしてそこまでのコードを対称に折り返す操
作を繰り返すことにより、このコードは生成
される。2 進コードからグレイコードへの変
換は簡単である。列を右に1文字シフトして、
元の列とビットごとの排他的論理和(異なれ
ば 1、等しければ 0)をとればよい。これは、
本誌1997年9月号で、大久保剛史さんが紹介
されていたコードそのものである。大久保さ
んの記事と多少重複するが、グレイコードの
性質について、少しみてみよう。
2進法では、 0111 の後は 1000 という具合
いに、1を加えることにより、多くの文字が
同時に変化する時がある。しかし、グレイコー
ドでは、必ず1文字しか変化しない。この性
質をもつコードを総称してグレイコードとい
よび、表1のものは、反転グレイコードと呼
ぶこともある。この性質を利用して、連続に
変化する値を測定してデジタル値として出力
するセンサーの出力にグレイコードがよく用
いられる。センサーの入力が微妙に変化した
だけで出力の複数の桁が同時に変わると、そ
の変わった瞬間の出力を取り込んだ機器が、
とんでもなく違った値に解釈する恐れがある。
グレイコードを用いると、その心配はない。
また、構成方法からも分かるように、このコー
ドは高い対称性を持っている。2桁、3桁、...
のグレイコード表で、1を加える操作で何ビッ
ト目が変化するか書き並べていくと、121、
1213121、121312141213121、... と、対称
に成長していく列ができる。この列は、見た
目にも綺麗だし(1,2,3 を A, B, C で表す
と音楽のロンド形式だ)、また、n が n 枚目
の円盤の移動を示すとすると、これらはハノ
イの塔の解の手順と見ることもできる。このように、グレイコー
ドは、ゲームの解法などでよく登場するし
(1)、電子回路の最小化や画像圧縮といった、計算機科学の様々な分野
で応用されている。
連続で対称なのは美しいが、それでも我々が日常使わないのは、自然数が、元来、
対称なものではなく、0 から無限大に向けた方向性を持ったものだからだろう。
10進のグレイコードも同様に考えられるが、0,1,2,...,9 の後、19,18,... と逆
戻りするのはこの方向性に反している。グレイコードでの足し算などの演算も、
2進コードみたいに簡単にいかない。何よりも、 0999 から 1000、1999 から
2000 と、カウンターの全ての数字が同時に変わるのは、見てる人を楽しませて
くれる。
さて、次に、実数について考えてみよう。実
数は 0 と 1 の有限列としては表現できない
が、無限列としてなら表現できる。この場合
も、通常は 2 進展開が用いられるが、グレ
イコード展開というものも同様に考えられる。
上記の2進コードからグレイコードへの変換
手続きは無限列にも適用できるので、それを
2進展開に対して適用すれば、実数のグレイコード
展開が得られる。
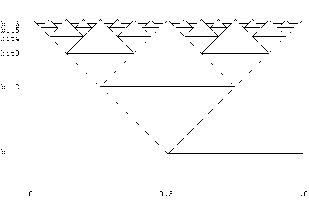
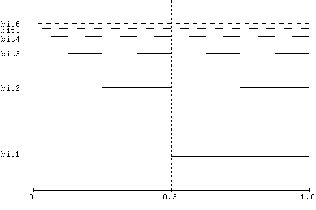
図 2 と図 3 に、(0,1) 区間の2
進展開とグレイコード展開を並べてみた。
図 2 を 1 ビット上にずらして元の図と xor を
とると 図 3 になることを確かめられたい。こ
の図で、線を引かれた部分はそのビットが
1,それ以外の部分は 0 であることを意味し
ている。(図 3 の斜めの線は、図をきれいに
見せるための補助線である。)図3のように、
グレイコード展開は、いたるところ対称な、
フラクタルな構造を持っている。
2 進展開は、k/2^{m} (k, m は整数)と
いう形で表現できる数(2進小数と呼ぶことに
する)に対して2つづつ存在する。たとえ
ば、1/2 には、0.100000... と
0.011111... という2進展開がある。よって
、グレイコード展開も2つづつ
存在することになる。1/2 のグレイコード
展開は、0.110000... と
0.010000... となる(図2,3の点線を参
照)。これらを比べると、2進では無限個の文
字が違っているが、グレイコードでは1文字
しか違わないことが分かる。
このことは、
次のようにも考えられる。図3の左半分(x < 1/2) の2ビット目から
先は図3全体を半分に縮小したもの、右半分(x > 1/2) の
2ビット目から先は図3全体を半分に縮小して反転したのになってい
る。このように、右半分を引っくり返すことにより、真ん中
のところで連続につながるようにしているのである。
興味深いことに、このグレイコード展開は、カオス理論で
よく知られている概念と一致している。上の考察より、
[0,1] 区間上で、グレイコード表現の最初のビッ
トを取り除くという操作は、次の関数
(テント関数として知られている)となる。
f(x) = 2x (0 ≦ x ≦ 1/2)
2(1-x) (1/2 ≦ x ≦ 1)
よって、x のグレイコード展開の n ビット目の値が 0 であ
るか 1 であるかは、x に f を n 回適用した値が 1/2 の左
にあるか右にあるかを示していることになる。その列(
すなわちグレイコード展開)は、f による旅程と呼ばれ、力学系の性質
を調べる基本的な道具となっている(2), (3)。
実数計算は、近似計算なら右から左に計算で
きるので2進展開の方が容易だが、無
限列のまま計算しようとすると、左から右に
計算を進める必要がある。その時、2 進展開
だと、例えば、引数を3倍するという計算を
1/6 = 0.0010101...に対して行うと
0.01111... か 0.10000... を出力し
ないといけないが、入力の有限部分を読み込
んだだけでは、どちらを出力していいか分か
らず、1文字も出力できないという問題が生
じる。その点、グレイコードだと、1桁目は
不定だが、2桁目から先は、100000... と一
意に定まり、1桁目を飛ばせば、出力可能と
なる(4)。このように、実数の計算を考
えるのに、グレイコードの方が都合がいいこ
とがある。また、連続性、対称性というのは、
まさに実数の性質であり、そういう性質
をコードの中に保持したグレイコードは、私
にはとても自然に見える。
(1)マーチン.ガードナー, 数学ゲームII, 別冊サイエンス31, 日本評論社 (1980).
(2)山口昌哉, カオスとフラクタル, ブルーバックスB-652, 講談社, 1986
(3)R.L.Devaney, 後藤憲一訳, カオス力学系入門第2版, 共立出版, 1990
(4)立木秀樹, 実数の表現とグレイコード, 数理科学11月号, pp26--33,(1999).

