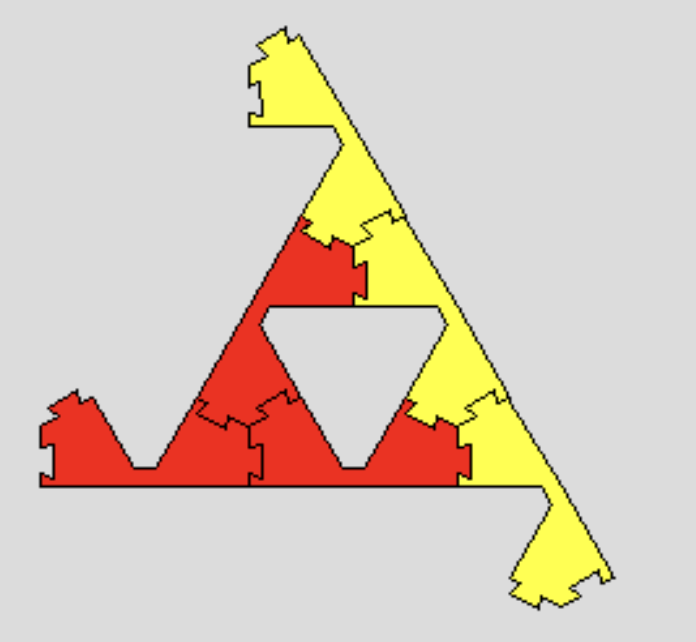
Sierpinski Triangle

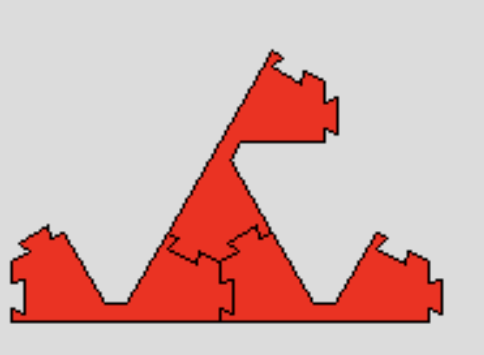
Clearly, a shape without open connectors is a collection of regular triangles. There are four ways to form a regular triangle by connecting three pieces. The following pictures show two of them, which we call Lions. The other two are called Mitsu-Mata, and are explained in the next page.
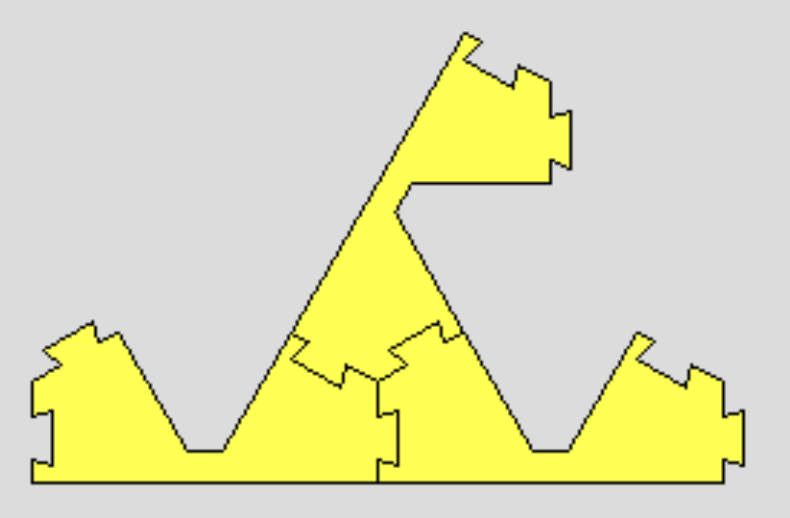
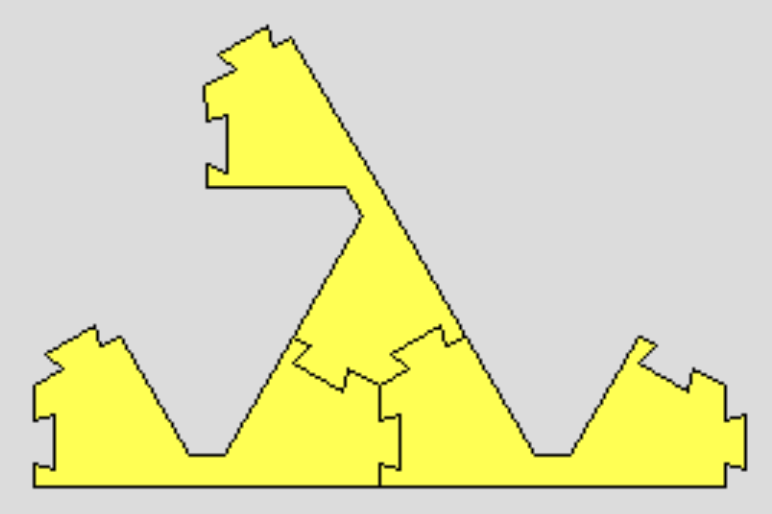
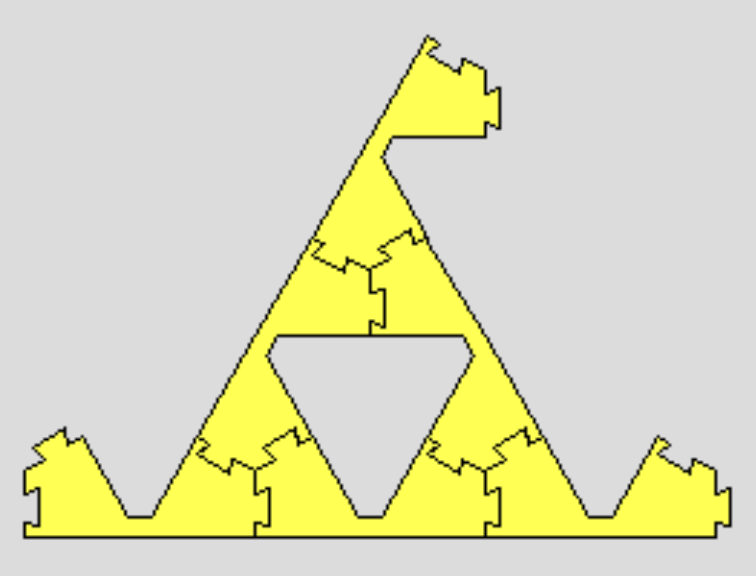
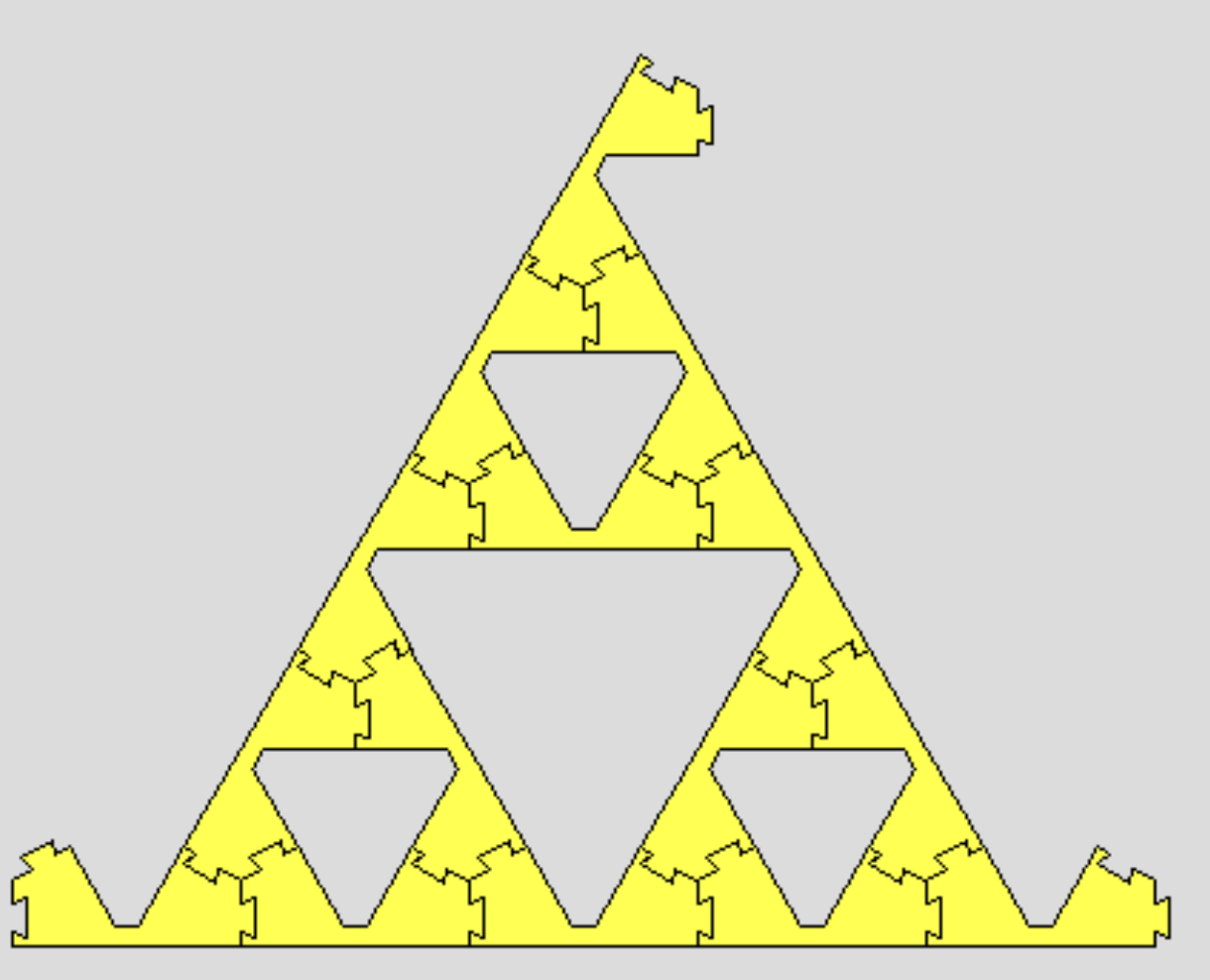

Our goal is to find an infinitely large shape without open connectors. Consider a sequence S0 ⊆ S1 ⊆ ...⊆ Sn ⊆ ... of level-n Sierpinski triangles and consider their union S. S almostly satisfies our requirement, but for the sequence we generated above, the leftmost connector is unchanged and it is left as an open connector of S. Therefore, one needs to connect something to this connector to obtain a shape without an open connector. One way is to form another sequence starting with forming a Lion on this connector. Another way is to connect three copies of them to a Mitsu-Mata (or its subspecies).
Here, we considered, as the following figure A shows, a level-1 approximation with the right and the top connectors facing each other. We have three possibilities of extending the red Lion to level-1 approximations, as the figures A, B, C shows. Here, the left and top connectors are facing each other in figures B and C, and the right connector is facing upwards in B and facing downwards in C.
 B
B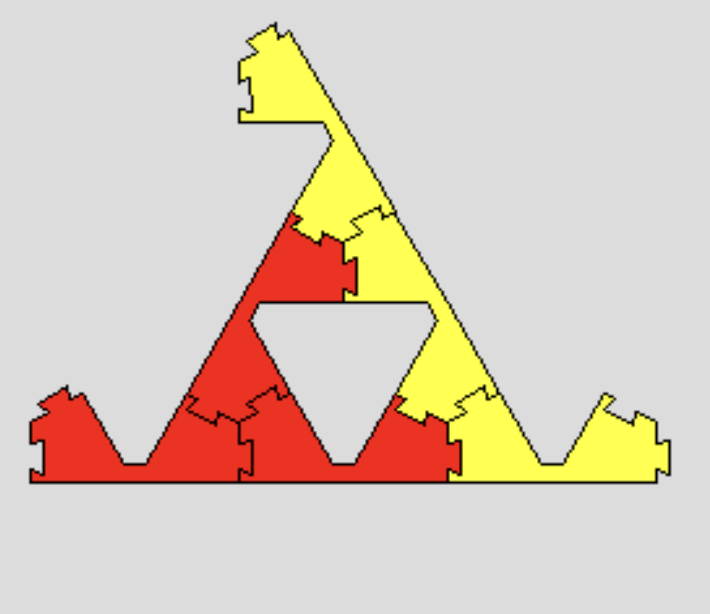 C
C