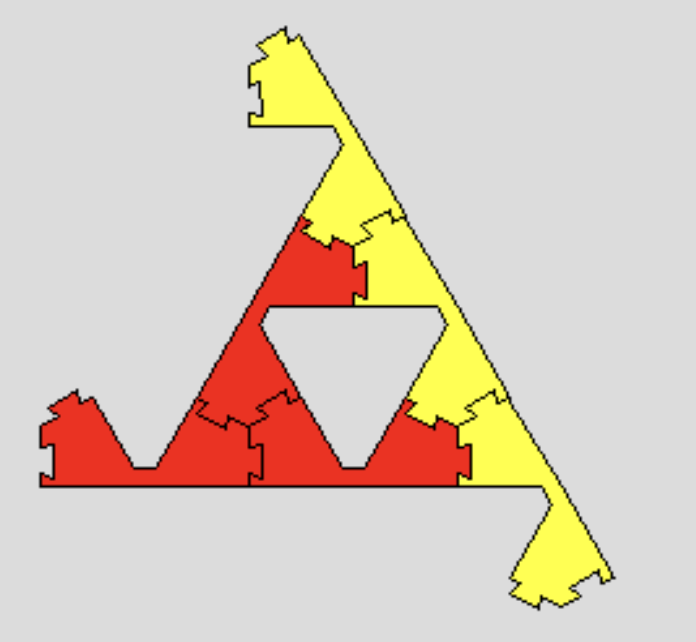
シェルピンスキー三角形
接続辺を残さないようにつなげると, 3個づつのピースが正三角形を作ります。 3 つのピースをつなげて正三角形を作る方法は,次の2通り (大きく口をあけた感じがするので,ライオンと呼ぶことにします) と,次のページで述べる2通り(三又)があります。
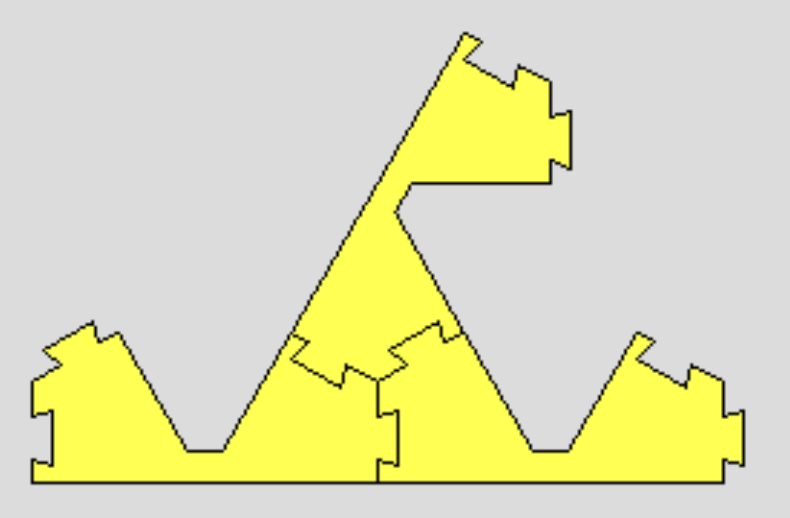
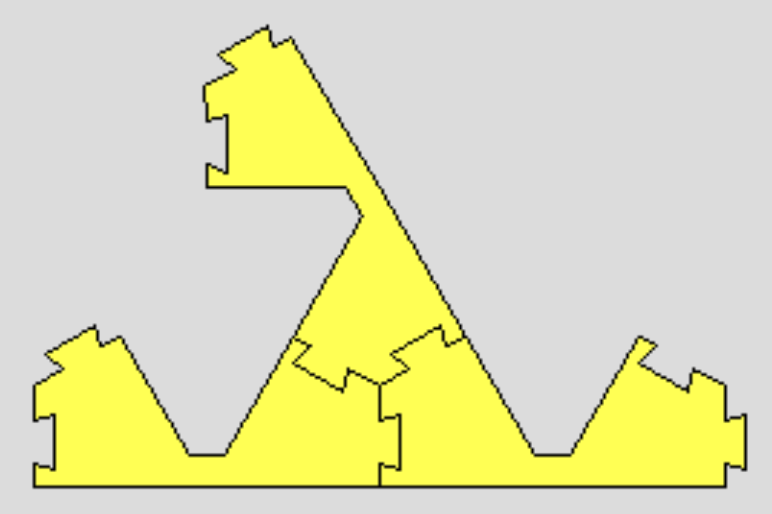
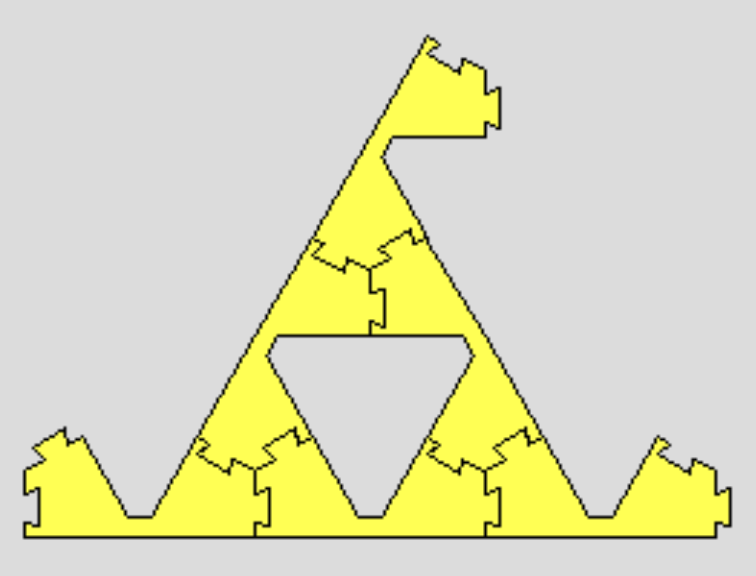
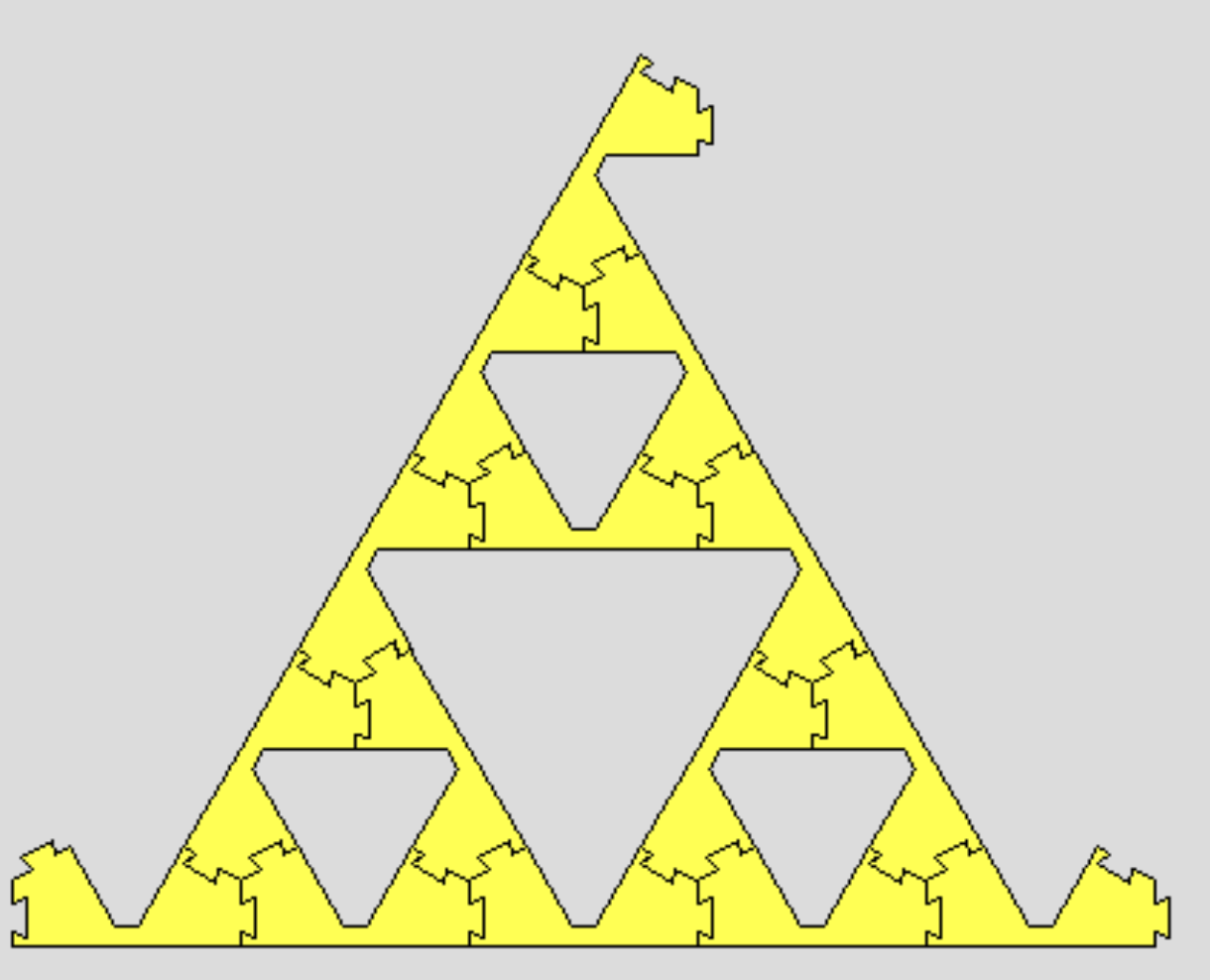


さて,今求めているのは,接続辺が残っていない,無限に大きな図形です。上の構成を 無限に繰り返して,レベル 4, 5, ... と無限に大きくしていったものを考えれば良さそうですが, それでは,右上に広がっていくだけで,左下のコネクターは何もつながらずに残ってしまいます。ですので,左下のコネクターの先にも同様のものを作ってつなげる必要があります。 それは,反対向きのライオンからはじめてもいいですし, あるいは,前ページの写真の真ん中にあげたように,「三又」(や,その亜種)に3つつなげていくこともできます。このようにしてできた,"無限に大きなシェルピンスキー三角形を2 つ,あるいは 3つつなげた形は,このピースからできる無限に大きな形です。
ここでは,レベル1の近似図形として,スタートのライオンと同じく,右と上のコネクターがお互いに向き合ったもの(A)を考えました。実は,この時点でのコネクターの作りに3通りの可能性があり,左と上のコネクターが向き合い,右のコネクターが上を向くもの(B)と下を向くもの(C)も作れます。
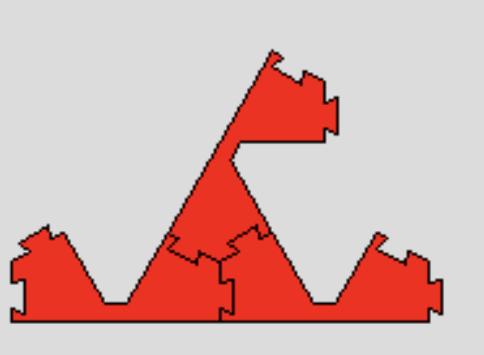
 B
B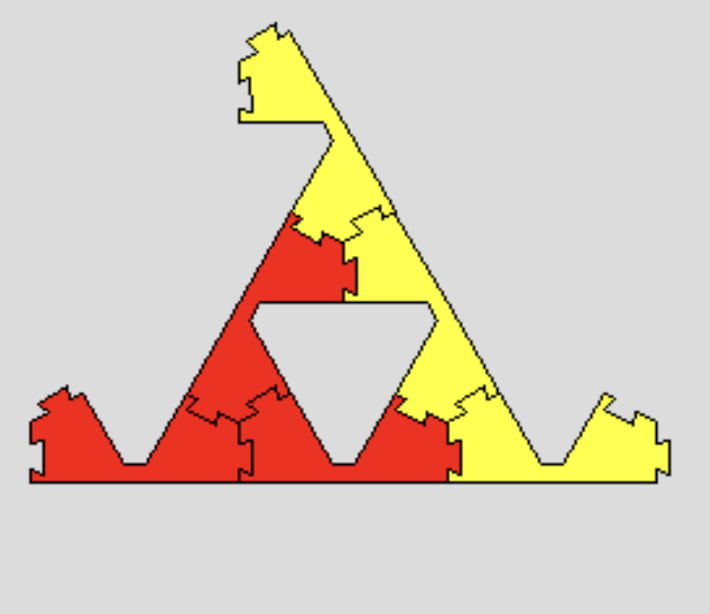 C
C