TriMata (三又)

京都大学人間・環境学研究科
立木秀樹


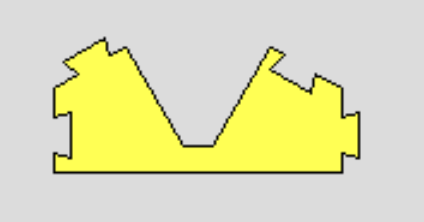
次の図形を接続辺（凸凹のある辺）で つなげていくと，どんな図形ができるでしょう？


黄色のピースの右の2つの接続辺へのつなげ方
接続辺が残らないようにつなげていくことを考えるのですが， 接続辺が全く残っていない作品を有限個のピースから作るのは不可能です。そこで，下図のような行き詰まりが起きないように，ピースの塊をどんどん大きくしていくことを考えましょう。


赤いピースの右向きのヘッドには何もつなげられない
TriMata で作られる形の一例です。
[シェルピンスキーの写真を追加]

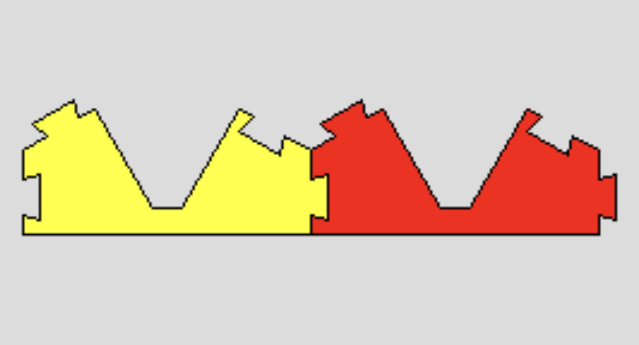
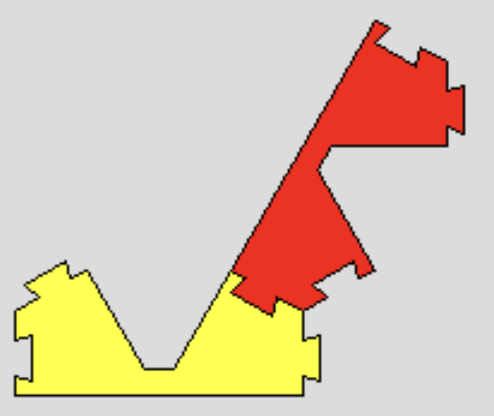
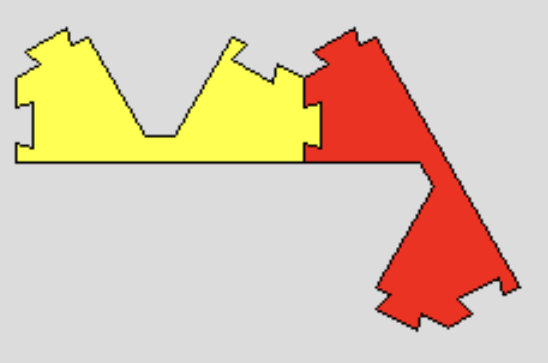
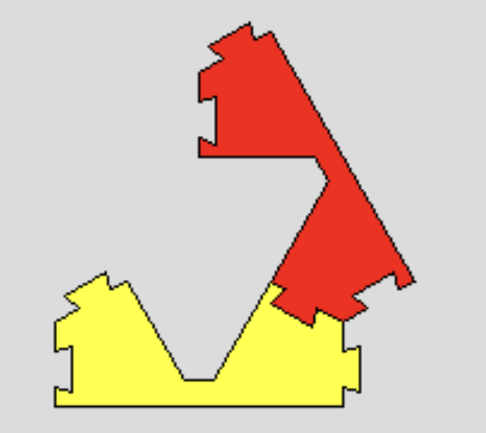
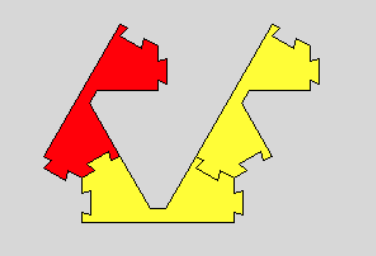
このピースは，他にも「予期しない」つなげ方が考えられます。 制限をつけずに遊ぶと，いろんな形ができて創造性がかきたてられます。写真ページのワークショップでの子供達の作品をご覧ください。

数学的背景：

このピースは，正三角形を三等分してできるたこ形を2つ棒でくっつけた形です。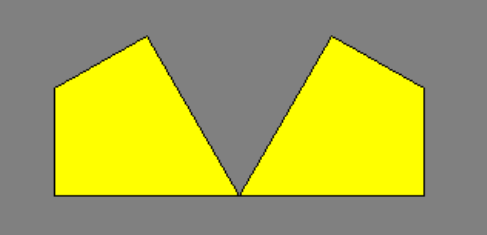
接続辺をつなげやすくするために，凹凸をつけてあります。 もし，凸と凸，凹と凹の辺をつなげて接続辺が残らない図形を作ろうとしても， すぐに行き詰まってしまいます。ですので， 凹凸をつけた接続辺で考えても，凹凸のない接続辺で考えても， 接続辺が残らないようにつなげてできる図形は同じです。

実は，これで作られる図形は，ルール18の（3方向）セルオートマトン(Cellular Automaton) が作る図形と一致しています。 Automaton の複数形が Automata であることや，上のような3回対象の写真の真ん中の黄色い図形（三又と呼ぶことにします）が作れることから，このパズルに TriMata (三又) という名前をつけました。