曲線・曲面の表現
曲線あるいは曲面を表現する方法はいくつかあります.
陰関数表現
3次元あるいは2次元空間での方程式(系)で与えられる制約を満たす点の集合として表すことができる曲線・曲面があります. そのような表現を陰関数表現といいます. たとえば,次のように定義されるf(x,y,z)=0という集合は,原点中心の半径rの球面を表します.
f(x,y,z) = x2+y2+z2 - r2 = 0
さらに次のg(x,y,z)=0という条件を追加すると円となります.
g(x,y,z) = ax+by+cz = 0
陽関数表現
次のように,曲線・曲面上の点の座標のうちのいくつかの成分の値が他の成分の値の関数で表現されている場合,そのような表現を陽関数表現といいます.
z = f(x,y) # 曲面 (y,z) = (p(x)q(x)) # 空間曲線 y = a(x) # 平面曲線
パラメトリック表現
曲線・曲面の各点の座標が,あるパラメタあるいはパラメタの組の関数で与えられる場合,そのような表現をパラメトリック表現といいます.
(x,y,z) = (f(t),g(t),h(t)) # パラメトリック曲線 (x,y,z) = (p(u,v),q(u,v),r(u,v)) # パラメトリック曲面
ベジェ曲線,ベジェ曲面
ベジェ(Bézier)曲線は,CGで用いられる代表的な曲線の一つで,次のように定義されます.
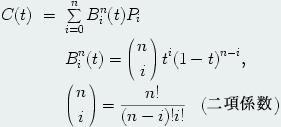
この定義に現われているnをベジェ曲線の次数といいます. またパラメタtの多項式をn次のベルンシュタイン(Bernstein)多項式といいます. n次のベジェ曲線はn+1個の制御点で定められます. ベジェ曲線は凸結合曲線であり,制御点のなす凸包に含まれます. また両端点は,それぞれ最初と最後の制御点に一致します. なお,CGでは,3次のベジェ曲線がよく使われます.
ベジェ曲面はベジェ曲線と同様にベルンシュタイン多項式を使って定義されます.
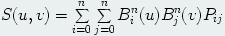
サンプルプログラム
ここでサンプルプログラム(bezier_curve.rb)を見て下さい. 各行の左端の数字は,説明のために付けた行の番号で,プログラムにはこの行番号は含まれません.
このプログラムでは,3次ベジェ曲線をその制御点とともに表示します. 制御点はマウスの左ボタンで掴んでドラッグにより動かすことができます. それにともない,曲線の形状も変化します. また次のような操作を行うことができます.
- [v]: 制御点をつなぐ破線表示のON/OFF
- [r]: 最初の状態に戻す.
- [q],[ESC]: プログラム終了
001 # coding: utf-8
002 require "opengl"
003 require "glu"
004 require "glut"
005
006 NPOINTS=100 # ベジェ曲線の近似に使用する点の数
007 WSIZE=600 # 初期ウインドウサイズ
008 PSIZE=5 # 制御点の描画サイズ(ピクセル単位)
009 NEAR=PSIZE+2 # 制御点の近傍の大きさを表す値
010
011 MIN_N=2
012 DEFAULT_N=4
013 def deploy_cpoints(n,r)
014 raise "#points >= #{MIN_N} is expected" if n < MIN_N
015 theta = 2*Math::PI/n
016 phi = theta/2
017 cp = []
018 n.times do |k|
019 t = k*theta+phi
020 x = r*Math.sin(t)
021 y = -r*Math.cos(t)
022 cp.push([x,y,0])
023 end
024 cp
025 end
026
027 N=(ARGV.size > 0) ? ARGV.shift.to_i : DEFAULT_N
028
029 CPPOS=0.5
030 # ベジェ曲線の制御点
031 __ctrl_points = deploy_cpoints(N,CPPOS)
032 # 制御点数
033 CPOINTS=__ctrl_points.size
034
035 # 制御点の初期状態を保存しておく(reset機能を実現するため)
036 __initial_ctrl_points = __ctrl_points.collect { |cp| cp.dup }
037
038 # 制御点をつなぐ破線のON/OFF
039 __draw_segments = false
040
041 # ウインドウの幅と高さ
042 __width = WSIZE
043 __height = WSIZE
044
045 # ドラッグされている点
046 __picked = nil
047
048 #### 表示コールバック ########
049 display = Proc.new {
050 GL.Clear(GL::COLOR_BUFFER_BIT)
051 # 制御点をつなぐ破線の描画
052 if __draw_segments
053 GL.Color(0.2,0.6,0.3)
054 GL.Enable(GL::LINE_STIPPLE) # 破線の描画を有効にする
055 GL.Begin(GL::LINE_STRIP)
056 CPOINTS.times do |i|
057 GL.Vertex(__ctrl_points[i])
058 end
059 GL.End()
060 GL.Disable(GL::LINE_STIPPLE) # 破線の描画を無効にする
061 end
062 GL.Color(0.9,0.1,0.0)
063 # 曲線の描画
064 # GL.EvalMesh1(style,first,last)
065 # style: 描画スタイル(GL::LINE,GL::POINT)
066 # first: 使用する(定義ずみ)グリッドのうちの最初の点の番号
067 # last: 使用する(定義ずみ)グリッドのうちの最後の点の番号
068 # ※ グリッド(曲線上に設置する点列に対応するパラメタ列)は,GL.MapGrid1d()で定義する
069 GL.EvalMesh1(GL::LINE,0,NPOINTS)
070 GL.Color(0.1,0.3,0.9)
071 # 制御点の描画
072 GL.Begin(GL::POINTS)
073 CPOINTS.times do |i|
074 GL.Vertex(__ctrl_points[i])
075 end
076 GL.End()
077 GLUT.SwapBuffers()
078 }
079
080 #### キーボード入力コールバック ########
081 keyboard = Proc.new { |key,x,y|
082 case key
083 # [d]: 制御点の出力
084 when 'd'
085 $stderr << "--- control points -------------------\n"
086 __ctrl_points.each_with_index do |cp,i|
087 $stderr << "%d %+.3f %+.3f %+.3f\n" % [i,cp[0],cp[1],cp[2]]
088 end
089 $stderr << "--------------------------------------\n"
090 # [v]: 制御点をつなぐ破線の描画ON/OFF
091 when 'v'
092 __draw_segments = (not __draw_segments)
093 GLUT.PostRedisplay()
094 # [r]: 制御点を初期状態に戻す
095 when 'r'
096 __ctrl_points.each_with_index do |cp,i|
097 cp.replace(__initial_ctrl_points[i])
098 end
099 __picked = nil
100 # 新しい制御点のもとでベジェ曲線を更新する
101 setup_curve(__ctrl_points)
102 GLUT.PostRedisplay()
103 # [q],[ESC]: 終了する
104 when 'q'
105 exit 0
106 end
107 exit 0 if key.ord == 0x1b
108 }
109
110 #### マウス入力コールバック ########
111 mouse = Proc.new { |button,state,x,y|
112 if button == GLUT::LEFT_BUTTON
113 # 左ボタンが押されたら,制御点を掴んでいるかどうかをチェックする
114 if state == GLUT::DOWN
115 # 各制御点がマウスポインタに十分近いかどうかを調べる.
116 # そのような制御点があったら,それを掴んだことにする.
117 __ctrl_points.each_with_index do |cp,i|
118 if near_enough(cp,x,y,__width,__height)
119 __picked = i
120 break
121 end
122 end
123 else # 左ボタンが離されたら,掴んでいた制御点を「離す」
124 __picked = nil
125 end
126 end
127 }
128
129 #### マウスドラッグコールバック ########
130 motion = Proc.new {|x,y|
131 # 制御点を掴んでいるときに,制御点の位置を更新する.
132 # またそれに合わせて曲線を更新する.
133 if __picked
134 # 制御点の位置をウインドウ座標(x,y)に対応する世界座標に更新する
135 __ctrl_points[__picked][0] = (2.0*x-__width)/WSIZE
136 __ctrl_points[__picked][1] = (__height - 2.0*y)/WSIZE
137 # 新しい制御点のもとでベジェ曲線を更新する
138 setup_curve(__ctrl_points)
139 GLUT.PostRedisplay()
140 end
141 }
142
143 #### ウインドウサイズ変更コールバック ########
144 reshape = Proc.new { |w,h|
145 GL.Viewport(0,0,w,h)
146 GL.LoadIdentity()
147 x=w.to_f/WSIZE
148 y=h.to_f/WSIZE
149 GLU.Ortho2D(-x,x,-y,y)
150 # ウインドウサイズデータを更新する
151 __width = w
152 __height = h
153 GLUT.PostRedisplay()
154 }
155
156 # 世界座標での(cp[0],cp[1])にウインドウ座標の(x,y)が十分近いかどうかを調べる
157 # ただしw,hはウインドウサイズ
158 def near_enough(cp,x,y,w,h)
159 u = (0.5*(WSIZE*cp[0] + w)).round
160 v = (0.5*(h - WSIZE*cp[1])).round
161 ((u-x).abs < NEAR) && ((v-y).abs < NEAR)
162 end
163
164 # 与えられた制御点列(ctrl_points)を使ってベジェ曲線を設定する
165 def setup_curve(ctrl_points)
166 # GL.Map1d(entity,t0,t1,stride,n,cpoints)
167 # entity: ベジェ曲線で生成するデータの種類
168 # (例) GL::MAP1_VERTEX_3: 3次元座標
169 # GL::MAP1_COLOR_4: (R,G,B,A)
170 # GL::MAP1_NORMAL: 法線ベクトル
171 # GL::MAP1_TEXTURE_COORD_1: テクスチャ座標(s)
172 # GL::MAP1_TEXTURE_COORD_2: テクスチャ座標(s,t)
173 # t0: パラメタの最小値
174 # t1: パラメタの最大値
175 # stride: ある制御点と次の制御点の間に並ぶデータ数(3次元座標なら3,RGBAなら4など)
176 # n: 制御点数(=ベジェ曲線の次数+1)
177 # cpoints: 制御点データ(全制御点の座標を順に並べた数値の列)
178 # ちなみに下で使われているflattenメソッドは,入れ子になっている
179 # 配列を「平ら」にする
180 # (例) [[1,2,[3]],4].flatten ==> [1,2,3,4]
181 GL.Map1d(GL::MAP1_VERTEX_3,0.0,1.0,3,CPOINTS,ctrl_points.flatten)
182 end
183
184 ##############################################
185 # main
186 ##############################################
187 GLUT.Init()
188 GLUT.InitDisplayMode(GLUT::RGB|GLUT::DOUBLE)
189 GLUT.InitWindowSize(__width,__height)
190 GLUT.CreateWindow("Bezier Curve")
191 GLUT.DisplayFunc(display)
192 GLUT.ReshapeFunc(reshape)
193 GLUT.KeyboardFunc(keyboard)
194 GLUT.MouseFunc(mouse)
195 GLUT.MotionFunc(motion)
196
197 setup_curve(__ctrl_points) # ベジェ曲線の設定
198 # グリッド(曲線上に設置する点に対応するパラメタの列)を設定する
199 # パラメタ値は等間隔に設定される
200 # GL.MapGrid1d(n,t0,t1)
201 # n: 設置するパラメタ区間数(n区間設置する.点の数はn+1となる)
202 # t0: 最初の点に対応するパラメタ値
203 # t1: 最後の点に対応するパラメタ値
204 GL.MapGrid1d(NPOINTS,0.0,1.0)
205 GL.Enable(GL::MAP1_VERTEX_3) # 曲線を利用可能にする
206 GL.PointSize(PSIZE) # 描画する点のサイズを設定する
207 # 破線描画のパターンの指定
208 # GL.LineStipple(factor,pattern)
209 # factor: patternの増幅パラメタ.
210 # pattern中の0の個数と1の個数をそれぞれfactor倍に増やす.
211 # たとえば,001110を2倍すると「000011111100」となる.
212 # pattern: 線分のパターン指定.4桁の16進数で指定する.
213 # それらを2進数に変換して下位ビットから読んだものがパターンとなる.
214 # 0は描画しない,1は描画するという意味に解釈される.
215 # (例) dddd ==> 1101110111011101(1101が4個)
216 # パターンは下位ビットから読んで,1011101110111011
217 # なお,下の例で「0x」は16進数を意味する接頭語である.
218 GL.LineStipple(2,0xdddd)
219 GL.LineWidth(2.0)
220 GL.ClearColor(1.0,1.0,1.0,0.0)
221 GLUT.MainLoop()
破線の描画
OpenGLでは,線分にパターンをつけて描くことができます. パターンを調整することで,破線や点線を描くことができます. パターンは,GL.LineStippleで定義します.
207 # 破線描画のパターンの指定
208 # GL.LineStipple(factor,pattern)
209 # factor: patternの増幅パラメタ.
210 # pattern中の0の個数と1の個数をそれぞれfactor倍に増やす.
211 # たとえば,001110を2倍すると「000011111100」となる.
212 # pattern: 線分のパターン指定.4桁の16進数で指定する.
213 # それらを2進数に変換して下位ビットから読んだものがパターンとなる.
214 # 0は描画しない,1は描画するという意味に解釈される.
215 # (例) dddd ==> 1101110111011101(1101が4個)
216 # パターンは下位ビットから読んで,1011101110111011
217 # なお,下の例で「0x」は16進数を意味する接頭語である.
218 GL.LineStipple(2,0xdddd)
サンプルプログラムに関する余談
サンプルプログラムでは,マウスで制御点を移動させる仕組みを用意しています. そのため,マウスで制御点をつかんだかどうかという処理,またウインドウ座標と世界座標を変換する処理を行っています. このプログラムは期待通りに動作するかと思いますが,あちこちに生の数字が入り込んでいるため,あまりスマートなものとはなっていません(これまでのサンプルもたいがいそういうところがありましたが,今回のものは,その程度が大きくなっています).
ベジェ曲線の生成と描画
OpenGLでベジェ曲線を扱う際には,まず1次元評価子(evaluator)を設定する必要があります. このとき,ベジェ曲線のパラメタの範囲,次数,制御点の座標を指定します. また,ベジェ曲線を適用する対象(entity)も指定します. ベジェ曲線で生成できるのは,3次元あるいは2次元空間内のいわゆる空間曲線だけではありません. 色,法線,あるいはテクスチャ座標といった対象(entity)のデータをベジェ曲線を使って指定することもできます. 評価子は,GL.Map1dによって設定します. なお,ベジェ曲線の対象(entity)は,GL.Enableによって,有効にしておく必要があります.
166 # GL.Map1d(entity,t0,t1,stride,n,cpoints)
167 # entity: ベジェ曲線で生成するデータの種類
168 # (例) GL::MAP1_VERTEX_3: 3次元座標
169 # GL::MAP1_COLOR_4: (R,G,B,A)
170 # GL::MAP1_NORMAL: 法線ベクトル
171 # GL::MAP1_TEXTURE_COORD_1: テクスチャ座標(s)
172 # GL::MAP1_TEXTURE_COORD_2: テクスチャ座標(s,t)
173 # t0: パラメタの最小値
174 # t1: パラメタの最大値
175 # stride: ある制御点と次の制御点の間に並ぶデータ数(3次元座標なら3,RGBAなら4など)
176 # n: 制御点数(=ベジェ曲線の次数+1)
177 # cpoints: 制御点データ(全制御点の座標を順に並べた数値の列)
178 # ちなみに下で使われているflattenメソッドは,入れ子になっている
179 # 配列を「平ら」にする
180 # (例) [[1,2,[3]],4].flatten ==> [1,2,3,4]
181 GL.Map1d(GL::MAP1_VERTEX_3,0.0,1.0,3,CPOINTS,ctrl_points.flatten)
:
205 GL.Enable(GL::MAP1_VERTEX_3) # 曲線を利用可能にする
評価子を設定したら,GL.EvalCoord1d(t)により.パラメタtの値でのベジェ曲線上の点の座標を得ることができます. そこで,折れ線を描画する要領でGL.Vertexで点を指定する代わりにGL.EvalCoord1dを用いれば,ベジェ曲線を折れ線で近似して描画することができます.
しかし,GL.EvalCoord1dのみを使って曲線を描くのは面倒です. そこで,OpenGLではパラメタ空間上で等間隔に並ぶ点を自動的に取りだして,それらに対応する曲線上の点を一つのメソッドで処理する仕組みが提供されています.
そのためには,予めGL.MapGrid1dで,パラメタ空間のどの範囲で,どれだけの点を設置するかを設定します. その後,それらの点に対応する曲線上の点をGL.EvalMesh1で描画します. なお複数のentityに対する評価子が設定されている場合,GL.EvalMesh1によって, それらの全てに対して処理が行われます.
063 # 曲線の描画
064 # GL.EvalMesh1(style,first,last)
065 # style: 描画スタイル(GL::LINE,GL::POINT)
066 # first: 使用する(定義ずみ)グリッドのうちの最初の点の番号
067 # last: 使用する(定義ずみ)グリッドのうちの最後の点の番号
068 # ※ グリッド(曲線上に設置する点列に対応するパラメタ列)は,GL.MapGrid1d()で定義する
069 GL.EvalMesh1(GL::LINE,0,NPOINTS)
:
:
198 # グリッド(曲線上に設置する点に対応するパラメタの列)を設定する
199 # パラメタ値は等間隔に設定される
200 # GL.MapGrid1d(n,t0,t1)
201 # n: 設置するパラメタ区間数(n区間設置する.点の数はn+1となる)
202 # t0: 最初の点に対応するパラメタ値
203 # t1: 最後の点に対応するパラメタ値
204 GL.MapGrid1d(NPOINTS,0.0,1.0)
ベジェ曲面の生成と描画
OpenGLでベジェ曲面を扱う際には,ベジェ曲線の場合と同様にまず2次元評価子(evaluator)を設定する必要があります. ベジェ曲線を適用する対象(entity), パラメタの範囲,次数,制御点の座標を指定することになります. 2次元評価子は,GL.Map2dによって設定します.
2次元評価子を設定したら,ベジェ曲線の場合と同様にGL.EvalCoord2d(u,v)によってパラメタu,vの値でのベジェ曲面上の点の座標を得ることができます. パラメタ空間上で等間隔に並ぶ点を自動的に取りだして,それらに対応する曲面 上の点を得るには,ベジェ曲線の場合と同様に,GL.MapGrid2dとGL.EvalMesh2とを使います.
サンプルプログラム(2)
ここでもう一つサンプルプログラム(bezier_surface.rb)を見て下さい. 各行の左端の数字は,説明のために付けた行の番号で,プログラムにはこの行番号は含まれません.
このプログラムは,指定されたテクスチャ画像を貼りつけたベジェ曲面を表示するものです. 次のように操作します.
- [j]/[J],[k]/[K],[l]/[L]で曲面の姿勢をさまざまに変えることができます.
- [z]/[Z]でカメラの原点からの距離を変えます.
- [r]で初期状態に戻ります.
- [t]で制御点の表示をON/OFFします.
- [q],[ESC]でプログラムを終了します.
001 # coding: utf-8
002 require 'opengl'
003 require 'glu'
004 require 'glut'
005 require 'cg/camera'
006 require 'cg/cpoints'
007 require 'cg/gfc'
008
009 INIT_THETA = 0.0 # カメラの初期位置
010 INIT_PHI = 0.0 # カメラの初期位置
011 INIT_DIST = 15.0 # カメラの原点からの距離の初期値
012 DT = 3 # 回転角単位
013 DZ = 0.125 # カメラの原点からの距離変更の単位
014 WSIZE = 600 # ウインドウサイズ
015 NSTEPS = 30 # 曲面を分割する区間の数(1方向)
016
017 __camera = Camera.new(INIT_THETA,INIT_PHI,INIT_DIST)
018
019 # 曲面の制御点
020 __surf_points = CtrlPointSet.new([
021 [[-3.0, 3.0, -2.0],[-1.0, 3.0,-1.0],[ 1.0, 3.0, 1.0],[ 3.0, 3.0, 2.0]],
022 [[-3.0, 1.0, -2.0],[-1.0, 1.0,-1.0],[ 1.0, 1.0, 1.0],[ 3.0, 1.0, 2.0]],
023 [[-3.0,-1.0, 2.0],[-1.0,-1.0, 1.0],[ 1.0,-1.0, -1.0],[ 3.0,-1.0,-2.0]],
024 [[-3.0,-3.0, 2.0],[-1.0,-3.0, 1.0],[ 1.0,-3.0, -1.0],[ 3.0,-3.0,-2.0]]])
025
026 # テクスチャ座標曲面の制御点(この場合は平面を作ることになる)
027 __tex_points = CtrlPointSet.new([[[0.0,0.0],[1.0,0.0]],[[0.0,1.0],[1.0,1.0]]])
028
029 # 制御点表示ON/OFF
030 __draw_cpoints = false
031
032 ## 制御点を球で描画する
033 SLICES=6
034 STACKS=6
035 SZ=0.1
036 SZ2=0.12
037 def draw_cpoints(cpoints)
038 GL.Material(GL::FRONT,GL::AMBIENT, [0.2,0.2,0.2])
039 GL.Material(GL::FRONT,GL::DIFFUSE, [0.2,1.0,0.4])
040 GL.Material(GL::FRONT,GL::SPECULAR, [0.0,0.0,0.0])
041 GL.Material(GL::FRONT,GL::SHININESS,0.0)
042 cpoints.each do |v| # 各制御点について
043 GL.PushMatrix()
044 # 平行移動してから球を表示する
045 # vは制御点の座標: v = [x,y,z]
046 GL.Translate(*v)
047 GLUT.SolidSphere(SZ,SLICES,STACKS)
048 GL.PopMatrix()
049 end
050 # アクティブな制御点を描画する
051 GL.Material(GL::FRONT,GL::AMBIENT, [0.2,0.2,0.2])
052 GL.Material(GL::FRONT,GL::DIFFUSE, [1.0,0.4,0.4])
053 GL.Material(GL::FRONT,GL::SPECULAR, [0.0,0.0,0.0])
054 GL.Material(GL::FRONT,GL::SHININESS,0.0)
055 v = cpoints.active
056 GL.PushMatrix()
057 GL.Translate(*v)
058 GLUT.SolidSphere(SZ2,SLICES,STACKS)
059 GL.PopMatrix()
060 end
061
062 # 曲面のデータのための評価子の設定
063 # entity: ベジェ曲面で生成するデータの種類
064 # points: 制御点集合
065 def map2d(entity,points)
066 # GL.Map2d(entity,u0,u1,u_stride,Nu,v0,v1,v_stride,Nv,cpoints)
067 # entity: ベジェ曲面で生成するデータの種類
068 # u0: uの最小値
069 # u1: uの最大値
070 # u_stride: u方向に関して制御点と次の制御点の間に並ぶデータ数
071 # Nu: u方向の制御点数
072 # v0: vの最小値
073 # v1: vの最大値
074 # v_stride: v方向に関して制御点と次の制御点の間に並ぶデータ数
075 # Nv: v方向の制御点数
076 # cpoints: 制御点データ列
077 # 全制御点の座標の二次元配列を順に一列に並べた数値の列
078 n_u = points.cols # Nu
079 n_v = points.rows # Nv
080 dim = points.dim # u_stride=dim, v_stride = u_stride*Nu
081 GL.Map2d(entity,
082 0.0,1.0,dim,n_u,
083 0.0,1.0,dim*n_u,n_v,
084 points.flatten)
085 end
086
087 #### 表示コールバック ########
088 display = Proc.new {
089 GL.Clear(GL::COLOR_BUFFER_BIT|GL::DEPTH_BUFFER_BIT)
090 GL.Light(GL::LIGHT0,GL::POSITION,[0.0,0.0,1.0,0.0])
091 GL.Light(GL::LIGHT1,GL::POSITION,[0.0,0.0,-1.0,0.0])
092
093 GL.Material(GL::FRONT_AND_BACK,GL::AMBIENT, [0.2,0.2,0.2])
094 GL.Material(GL::FRONT_AND_BACK,GL::DIFFUSE, [0.8,0.8,0.8])
095 GL.Material(GL::FRONT_AND_BACK,GL::SPECULAR, [0.0,0.0,0.0])
096 GL.Material(GL::FRONT_AND_BACK,GL::SHININESS,0.0)
097
098 # 曲面の評価子の設定(空間曲面,テクスチャ座標曲面)
099 map2d(GL::MAP2_VERTEX_3,__surf_points)
100 map2d(GL::MAP2_TEXTURE_COORD_2,__tex_points)
101
102 # 曲面の描画
103 # GL.EvalMesh2(style,u_first,u_last,v_first,v_last)
104 # style: 描画スタイル(GL::FILL,GL::LINE,GL::POINT)
105 # u_first: 使用する(定義ずみ)グリッドのうちのu方向の最初の点の番号
106 # u_last: 使用する(定義ずみ)グリッドのうちのu向の最後の点の番号
107 # v_first: 使用する(定義ずみ)グリッドのうちのv方向の最初の点の番号
108 # v_last: 使用する(定義ずみ)グリッドのうちのv方向の最後の点の番号
109 # ※ グリッド(曲面上に設置する点列に対応するパラメタ列)は,GL.MapGrid2d()で定義する.
110 GL.EvalMesh2(GL::FILL,0,NSTEPS,0,NSTEPS)
111
112 GL.Disable(GL::TEXTURE_2D)
113 draw_cpoints(__surf_points) if __draw_cpoints
114 GL.Enable(GL::TEXTURE_2D)
115
116 GLUT.SwapBuffers()
117 }
118
119 #### キーボード入力コールバック ########
120 keyboard = Proc.new { |key,x,y|
121 case key
122 # [j],[J]: 経度の正方向/逆方向にカメラを移動する
123 when 'j','J'
124 __camera.move((key == 'j') ? DT : -DT,0,0)
125 # [k],[K]: 緯度の正方向/逆方向にカメラを移動する
126 when 'k','K'
127 __camera.move(0,(key == 'k') ? DT : -DT,0)
128 # [z],[Z]: zoom in/out
129 when 'z','Z'
130 __camera.zoom((key == 'z') ? DZ : -DZ)
131 # [r]: 初期状態に戻す
132 when 'r'
133 __camera.reset
134 # [t]: 制御点表示のON/OFF
135 when 't'
136 __draw_cpoints = (not __draw_cpoints)
137 # [q],[ESC]: 終了する
138 when 'q'
139 exit 0
140 end
141 exit 0 if key.ord == 0x1b
142 GLUT.PostRedisplay()
143 }
144
145 #### ウインドウサイズ変更コールバック ########
146 reshape = Proc.new { |w,h|
147 GL.Viewport(0,0,w,h)
148 __camera.projection(w,h)
149 GLUT.PostRedisplay()
150 }
151
152 ### 曲面の設定 ########
153 def setup_surface
154 GL.Enable(GL::MAP2_VERTEX_3)
155 GL.Enable(GL::MAP2_TEXTURE_COORD_2)
156
157 # グリッド(曲面上に設置する点に対応するパラメタの列)を設定する
158 # パラメタ値は等間隔に設定される
159 # GL.MapGrid2d(Nu,u0,u1,Nv,v0,v1)
160 # Nu: u方向に設置する区間数(点の数は,Nu+1)
161 # u0: u方向の最初の点に対応するパラメタ値
162 # u1: u方向の最後の点に対応するパラメタ値
163 # Nv: v方向に設置する区間数(点の数は,Nv+1)
164 # uv: v方向の最初の点に対応するパラメタ値
165 # uv: v方向の最後の点に対応するパラメタ値
166 GL.MapGrid2d(NSTEPS,0.0,1.0,NSTEPS,0.0,1.0)
167 end
168
169 ### テクスチャの設定 ########
170 def setup_texture(iname)
171 ## テクスチャ画像の読み込み
172 g = Gfc.load(iname)
173 width,height = g.size
174
175 ## テクスチャ生成
176 GL.TexImage2D(GL::TEXTURE_2D,0,GL::RGB,width,height,0,GL::RGB,
177 GL::UNSIGNED_BYTE,g.get_bytes)
178
179 ## テクスチャ座標に対するパラメタ指定
180 GL.TexParameter(GL::TEXTURE_2D,GL::TEXTURE_WRAP_S,GL::REPEAT)
181 GL.TexParameter(GL::TEXTURE_2D,GL::TEXTURE_WRAP_T,GL::REPEAT)
182
183 ## ピクセルに対応するテクスチャの値の決定
184 GL.TexParameter(GL::TEXTURE_2D,GL::TEXTURE_MAG_FILTER,GL::NEAREST)
185 GL.TexParameter(GL::TEXTURE_2D,GL::TEXTURE_MIN_FILTER,GL::NEAREST)
186
187 ## テクスチャの環境(表示方法)の指定
188 GL.TexEnv(GL::TEXTURE_ENV,GL::TEXTURE_ENV_MODE,GL::MODULATE)
189
190 GL.Enable(GL::TEXTURE_2D)
191 end
192
193 ### シェーディングの設定 ########
194 def init_shading
195 GL.Light(GL::LIGHT0,GL::AMBIENT, [0.1,0.1,0.1])
196 GL.Light(GL::LIGHT0,GL::DIFFUSE, [1.0,1.0,1.0])
197 GL.Light(GL::LIGHT0,GL::SPECULAR,[1.0,1.0,1.0])
198
199 GL.Light(GL::LIGHT1,GL::AMBIENT, [0.4,0.4,0.4])
200 GL.Light(GL::LIGHT1,GL::DIFFUSE, [1.0,1.0,1.0])
201 GL.Light(GL::LIGHT1,GL::SPECULAR,[1.0,1.0,1.0])
202
203 GL.Enable(GL::LIGHTING)
204 GL.Enable(GL::LIGHT0)
205 GL.Enable(GL::LIGHT1)
206 GL.Enable(GL::NORMALIZE) # 法線の自動単位ベクトル化
207 GL.Enable(GL::AUTO_NORMAL) # 曲面の法線を自動生成する
208
209 GL.LightModel(GL::LIGHT_MODEL_TWO_SIDE,1) # 両面シェーディングモード
210 end
211
212 ##### main ##############################################
213 if ARGV.size == 0
214 STDERR.puts 'テクスチャ画像が指定されていません'
215 exit 1
216 end
217
218 GLUT.Init()
219 GLUT.InitDisplayMode(GLUT::RGB|GLUT::DOUBLE|GLUT::DEPTH)
220 GLUT.InitWindowSize(WSIZE,WSIZE)
221 GLUT.CreateWindow('Textured Bezier Surface')
222 GLUT.DisplayFunc(display)
223 GLUT.KeyboardFunc(keyboard)
224 GLUT.ReshapeFunc(reshape)
225 GL.ClearColor(0.4,0.4,1.0,0.0)
226 GL.Enable(GL::DEPTH_TEST)
227 setup_surface() # 曲面の設定
228 setup_texture(ARGV.shift) # テクスチャの設定
229 init_shading() # シェーディングの設定
230 __camera.set # カメラを配置する
231 GLUT.MainLoop()
 日置尋久(HIOKI Hirohisa)
Last modified: Sat Aug 07 00:24:04 JST 2021
日置尋久(HIOKI Hirohisa)
Last modified: Sat Aug 07 00:24:04 JST 2021