課題
ライフゲームは,以下で説明するように,予め決められたルールにしたがって,平面上に敷き詰められた「セル」の状態が周囲の「セル」の状態によって,刻々と変化していくシステムです. この課題では,ライフゲームのルールにしたがって,セルの状態の時間変化していく様子をアニメーションとして示すようにします.
授業で提供するライフゲームのライブラリを用いることで,ライフゲームのセルのデータは順次生成できるようにしています. そこで今回の課題ではライフゲームのシステムを作る必要はありません. 課題のプログラムでは,ライブラリによって生成されるデータに基づいて セルの時間変化の様子を順にアニメーション表示する仕組みを実現してください.
なおプログラム実行開始の時点ではライフゲームの初期状態を表示して, キー入力あるいはマウスクリックでアニメーションを開始するようにしてください. また一旦停止,再開もできるようにしてください.
事前準備
課題に取り組む前に,「仮想型端末(VDI)」で次の手続きを行ってください. 今回の課題のためにシステムの設定を一部更新します.
- PandAから次のファイルを「Home」にダウンロードしてください.
リソース > 01_設定ファイル > update_20250430.sh
-
端末(Terminal)で次のコマンドを実行してください.
$ bash update_20250430.sh ⏎
なお「$」は端末画面に最初から出ている「プロンプト」を表しています.これは入力しません.
このコマンドを実行すると,次のようにメッセージが表示されます.
+ cd /home/xxxxxxxx/lib/ruby/cg + for f in ${FILES[@]} (中略) Saving to: ‘mglutils.rb’ mglutils.rb 100%[[===================>] 2.20K --.-KB/s in 0s 2025-04-30 08:20:58 (961 MB/s) - ‘mglutils.rb’ saved [2249/2249] + /bin/rm -f update_20250430.shコマンドの実行後,ダウンロードしたファイル(update_20250430.sh)は削除されます.
なお,この「事前準備」は一度だけ行います. 2回以上行う必要はありません(2回以上行っても問題は起きません).
ライフゲームの概観
ライフゲームとは状態が時間変化するセルで構成されるシステムです. 平面上に縦横に敷き詰められている均質な正方形のセルがあって,各セルはそれぞれ0か1のどちらかの状態をとります. 状態1ではセルに生命体がいて,状態0ではセルには生命体がいないと解釈します. 各セルの状態は周囲のセルの影響のもとで単位時間ごとに変化していくように定められます. 各セルの生命体は,周囲のセルの生命体に影響をうけて状態が変化すると考えるわけです.
次の画面は実際のゲームの進行例を一部示しています. 画面中で小さな白い四角の一つ一つが状態が1のセル(生命体が存在するセル)を示しています.
 |
…→ |  |
…→ |  |
…→ |  |
時刻t(t=0,1,2,...)に対して, 当該のセルと周囲8個の合計3×3個のセルの時刻tでの状態に基づいて, 予め決められたルールのもとで時刻t+1での各セルの状態が決定されます.
状態変化の具体的なルールは「ライフゲームのルール」に示しておきます.
ライフゲームのルール自体は固定されていて,ごく単純です. しかし初期配置(t=0)でのセルの状態を決めて,ルールにしたがってセルの状態を変えていくと, 時刻が経過するにつれ,しばしば思いも寄らない変化のパターンが現れます.
なおこの授業のライフゲームでは,縦横に並ぶセルの個数は決めてあって,左右の端のセル,上下の端のセルは互いに隣接しているものとして扱います(左と右,上と下がつながっていると解釈するわけです). そのようにするのは,上下左右の端にあるセルを特別扱いすることを避けるためです.
課題の進め方
セルの初期データを適当に決めて, ライフゲームのルールにしたがって,各セルの状態をステップごとに順次更新していく仕組みをライブラリとして用意してあります. ライブラリには,各時刻での各セルの状態を順に計算するための処理を組み込んであります. そこで課題のプログラムにおいては,ライフゲームで各セルのデータがどう変化するのかを具体的に計算する処理を書く必要はありません.
この課題では,各時刻での各セルの状態はライブラリによって計算されることを前提として,セルの状態に基づいて画面を描いて, またライフゲームを自動的に1ステップずつ進行させていくプログラムを作成してください. キー入力あるいはマウスクリックでアニメーションを開始するようにして, 一旦停止,再開もできるようにしてください.
課題のために次のテンプレートを用意しています.
テンプレートには,ライフゲームを開始できるように準備する処理は記述してあります. 課題では,テンプレートに次の2つの処理を適宜追加して,プログラムを完成させてください.
- ゲームを1ステップ進行させる処理(ライブラリによるセルの状態更新を実行)
- 現在の各セルの状態に従って画面を描画する処理
アニメーションの実現については,次のサンプルプログラムも参考にしてください.
以下でゲームを進行させる方法とセルを描画する方法について,詳しく説明します.
ライフゲームのデータ管理
今回のプログラムでは状態変数__gameを用いて,ライフゲームに関するさまざまな処理を実行できるようになっています. ゲームの進行とセルの描画において,ともに__gameを利用します.
ゲームの進行(セルの状態更新)
ライフゲームを1ステップ進行して(時刻をt→t+1と進めて),全てのセルの状態を(一斉に)更新するには次を実行します.
| __game.step | ライフゲームを1ステップ進行させる |
|---|
__game.stepをプログラムで実行すると,ライブラリの内部で,すべてのセルの状態がライフゲームのルールにしたがって一斉に更新されます.
しかし__game.stepを実行した時点で画面が更新されるわけではありません. この__game.stepでは,セルごとの「生命体が存在する・しない」という状態を表すデータ(存在しない=0,存在する=1)を更新するだけです. 画面を更新するには,描画コールバック(display)において,セルを描画する処理を記述しておいて, __game.stepによって更新されたセルのデータにしたがって,画面を再描画する必要があります.
参考のために,テンプレートにはkeyboardコールバックの中で[s]を押したときにライフゲームを1ステップ進行させて,描画コールバック(display)の実行を予約する処理(GLUT.PostRedisplay())が組み込まれています(keyboardコールバックを参照のこと). 描画コールバック(display)が適切に記述されていれば,[s]を押すたびに各セルの状態が1ステップずつ更新されて,それに合わせて画面も更新されます.
このステップ動作([s]を押したときの処理)は,参考のために記述してあります.削除しても構いませんし,そのまま残しておいても構いません. このステップ動作とアニメーションとの干渉(アニメーション実行中に[s]を押したらどうなるか)は気にする必要はありません(この問題の解消のために何か工夫をすることも歓迎です).
セルの配置とセルの状態の確認
テンプレートではセルはN×N個配置されるようになっています(Nの値はテンプレートの最初に定義してあります). 下図に示すように,セルの位置を(i,j)で表すとi,jの範囲は0 ≦ i,j < Nとなっています. 左から右に向かってi=0,1,2,...,N-1,上から下に向かってj=0,1,2...,N-1となっていて,左上角が(0,0)で右下角が(N-1,N-1)です.
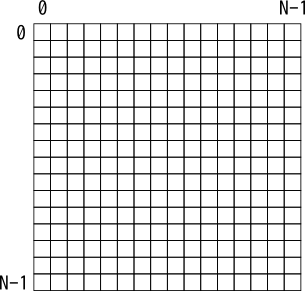
今回のプログラムでは__game.state(i,j)で(i,j)の位置のセルの状態(0か1)を知ることができるようになっています.
| __game.state(i,j) | (i,j)の位置のセルの状態(0か1)を調べる |
|---|
仮に「N = 4」であったとして,セルのデータが次のようになっていたとします.
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 |
この場合,たとえば__game.state(i,j)によって,次のように値が得られます.
s00 = __game.state(0,0) # s00 == 0 s30 = __game.state(3,0) # s30 == 1 s12 = __game.state(1,2) # s12 == 1
セルに対する処理を一般化して表現するための仕組み
今回の課題では,セルをN×N個用意したとして,描画処理を一般化して, Nがどんな値であれ,(それが適切な値であれば)プログラムの記述を変えることなく,各セルの状態を調べて,生命体が存在するセルを描画するようにできます. そのために次の仕組みを用意しています.
| [N,N].grid_points do |i,j| : : end |
N×N個のセルのそれぞれについて,do〜endの内部に記述されている処理を実行する.(i,j)がセルの位置を表す. |
|---|
N×N個のセルのそれぞれについて「do ... end」の内部の処理を実行します. 各セルは位置(i,j)で区別されます(i=0,1,...,N-1,j=0,1,...,N-1). 「do ... end」の内部では, (i,j)の位置にあるセルについて行う処理を,i,jを含む式を用いて一般的に記述できます.
さてテンプレートでは次のように記述してあります.
[N,N].grid_points do |i,j|
## 次のputsの行を有効にすると,セル(i,j)の状態をTerminal画面に表示する
## (※ 完成したプログラムには不要)
# puts "(#{i},#{j}):#{__game.state(i,j)}"
# セル(i,j)に生命体が存在する?
if __game.state(i,j) == 1
#
# 生命体が存在したときの描画処理を「if...end」の中に書く
#
end
end
ここでテンプレートのこの部分を次のように書き換えたとします(太字で表現しているのが書き換えた部分です).
[N,N].grid_points do |i,j|
## セル(i,j)の状態をTerminal画面に表示する
## (※ 完成したプログラムには不要)
puts "(#{i},#{j}):#{__game.state(i,j)}"
# セル(i,j)に生命体が存在する?
if __game.state(i,j) == 1
#
# 生命体が存在したときの描画処理を「if...end」の中に書く
#
end
end
ここではテンプレートの「puts」の行の「#」を削除しています(この変更に合わせて2行前のコメントも同時に書き換えていますが,動作には影響しません). この変更によって「puts」の行も実行されるようになります. 「puts」は,与えられた指示に従ってTerminalの画面にデータを表示します.
このよう書き換えたとしたとき,プログラムがどのように動作するかを説明するために, 仮に「N = 4」であったとして,セルのデータが次のようになっていたとします.
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 |
この場合に,上のプログラム([N,N].grid_points do ... end)が実行されたとすると, putsがN×N=4×4=16個のセルについて実行されて, Terminalの画面に次のように表示されることが想定されます.
(0,0):0 (1,0):0 (2,0):1 (3,0):1 (0,1):0 (1,1):0 (2,1):0 (3,1):0 (0,2):0 (1,2):1 (2,2):0 (3,2):0 (0,3):0 (1,3):0 (2,3):0 (3,3):1
このような結果になるのは, (i,j)=(0,0),(1,0),(2,0),(3,0),(0,1),...,(2,3),(3,3)のそれぞれの場合について,その(i,j)の値のもとで「do...end」の内部の処理が実行されるためです. この場合は「puts」によって,各(i,j)の組み合わせについてTerminalの画面にセル(i,j)の状態(__game.state(i,j))が表示されるわけです(if式の中には何も処理を書いていませんので,条件が正しい場合でも何も行われません).
なおputsの行の処理について説明すると,ここでのputsでは"......"で括られた「メッセージ」をTerminalに表示しています. このとき"......"の中に「#{式}」という指示があると,「式」の値を求めて,その結果で「#{式}」の部分を置き換えた「メッセージ」がまず作られます.それがputsで表示されることになります. たとえば上の図の4×4のセルの例で,(i,j)=(1,2)の場合はメッセージが次のように作られます.
# i==1,j==2, __game.state(1,2)==1 (上の図の例の場合)
"(#{i},#{j}):#{__game.state(i,j)}" ==> "(1,2):1"
セルの描画
以上の仕組みを使って,作成するプログラムでは,セルの位置(i,j)を利用して,その位置に生命体が存在する場合にのみ(つまり__game.state(i,j)==1の場合のみ),そのセルの位置に四角を描画します.
そのためにはセルの位置とOpenGLの画面の座標との対応を適切に定める必要があります. セルの位置,画面の座標系は次に示す通りです.
| セルの位置 | 画面の座標系 |
| iの範囲: i=0,1,...,N-1 | xの範囲: -1≦x≦1 |
| jの範囲: j=0,1,...,N-1 | yの範囲: -1≦y≦1 |
| (左上が原点,iは右向き,jは下向き) | (中心が原点,x軸は右向き,y軸は上向き) |
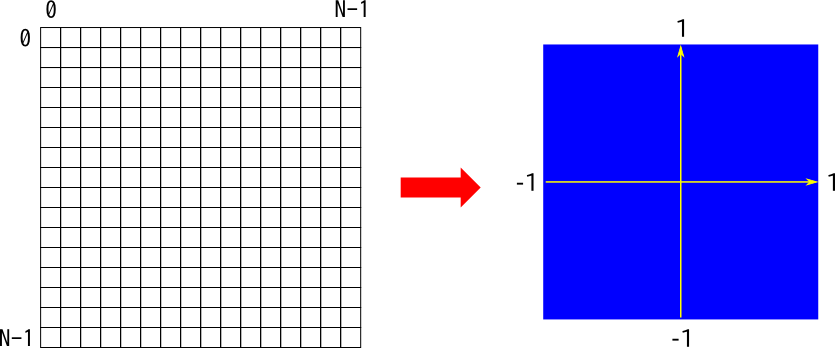
このときプログラムで指定している「1辺のセルの個数」であるNの値を変更してもプログラムが動作するように,描画処理はNを用いて記述しておくとよいでしょう.
四角を描画するにはGL.Rectを使うとよいでしょう.
# 左上角(x0,y0),右下角(x1,y1)の矩形を描く
GL.Rect(x0,y0,x1,y1)
プログラムの挙動を修正する手がかりを得る方法
たとえプログラムが動作しても,結果が想定通りにならないことはよくあります. そのような場合,プログラムに何らかの誤りがあるはずですが,プログラムの記述を調べたり,CGの画面を見るだけでは誤りが容易には見つけられないことも少なからずあります. そのようなとき,プログラム実行中に「誤りに関連がありそうな変数の値」を調べてみると,手がかりになりえます. 次を参考にしてみてください.
座標値の計算に関する注意
整数と整数で除算を行うと商が得られることに注意してください.
N = 64
i = 32
i/N # ==> 0 (0.5にはならない!)
整数を小数点数に変換すればこの問題を避けられます.
N = 64 i = 32 # 『整数.to_f』で整数を小数点数に変換できる i.to_f/N # ==> 0.5 # 除算の前に変換しないとやはり0になってしまう (i/N).to_f # ==> 0.0 k = 5 # 整数定数を使う場合は「.0」をつければよい(to_fを使う必要はない) 1.0/k # ==> 0.2 1/k # ==> 0
(参考)グリッドの描画
一つ一つのセルをはっきり区別するために枠線を描いてもよいかもしれません(課題では実現する必要はありません). これを実現するには画面を縦横に区切る線(グリッド)を描けばよいでしょう. 次のような繰り返し処理を利用すれば,これを簡単に実現できます. なお線を描くにはGL::LINESのプリミティブを使います.
N.times do |k|
# k = 0,1,...,N-1について(計N回),
# do...endの処理をそれぞれ実行する
end
(参考) ライフゲームでの実験
プログラムができたら,ライフゲームのパラメタを変えてみたり, 特別な初期配置からゲームを開始させたりしてみるとよいでしょう. パラメタとしては次の2つが調整可能です.
- RATE(初期配置に出現させる生命体の割合[0以上1以下])
- N(1辺のセルの個数)
(参考) 初期配置データファイル
今回のプログラムでは,生命体セルを特定のパターンに配置してからライフゲームを始めるようにできるようにもなっています. 興味があれば,以下のファイルをダウンロードして,次のように実行してみてください(プログラムファイル名をlg.rbとしています).
なおこれらのデータはライフゲームの情報サイト(Lifewiki)のページを参照して作成しました. 初期配置に関するLifewikiの解説ページへのリンクも示しておきます.
$ ruby lg.rb 初期配置ファイル名
(参考) ライフゲームのルール
ここではライフゲームでのセルの状態変化を定めるルールについて説明します. 課題のプログラムを実現するだけであれば,以下を参照する必要はありません.
時刻tでのセルの状態に対して, そのセルの時刻t+1の状態は,次の図のように,当該のセルと周囲8個を合わせた3×3個のセルの時刻tでの状態によって決められます.
状態変化のルールは次の表の通りです. あるセルの状態が次にどうなるかは, 周囲の8個のセルに「状態1」のセルが何個あるかで決められます.
| 周囲の「1」の個数 | セルの次状態 |
|---|---|
| 1個以下 | 0 |
| 2個 | 変化しない |
| 3個 | 1 |
| 4個以上 | 0 |
注目するセル(Cとします)の周囲に「状態1」のセルが1個以下または4個以上あるときは次状態は0, 3個のときは次状態は1になります(現在のセルCの状態には依存しません). また周囲に「状態1」のセルが2個のときはセルCの状態は変化しません. つまり現在の状態が0なら次状態も0,現在の状態が1なら次状態も1のままとなります.
すでに説明している通り,状態1のセルには生命体が存在して,状態0のセルは空である(生命体は存在しない)と考えてみます. このときライフゲームのルールを次のように解釈できます.
- 生命体は周囲が過疎(周囲の生命体が1個以下)でも,過密(周囲の生命体が4個以上)でも生き残れない(次に状態が0になる).
- 生命体は周囲の生命体の数がほどほど(周囲の生命体が2個か3個)であれば,生き残る(1の状態を保つ).
- 空のセルの周囲の生命体の数がちょうどよければ(周囲の生命体が3個),そこに新たな生命体が誕生する.
次にごく小さなライフゲーム(セルが4×4=16個)の進行の例をデータとして示します. 上で示したルールにしたがって,ステップごとにセルの状態が変わっていることを確かめてみてください. すでに説明した通り,今回は左端と右端,上端と下端のセルは隣接しているものとして扱っていることに注意してください.
| step 0 | step 1 | step 2 | step 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
→ |
|
→ |
|
→ |
|
参考文献・情報源
次にライフゲームの参考文献,情報源を示します.
- Lifewiki
- 『ライフゲイムの宇宙』[新装版]
ウィリアム・パウンドストーン 著,有澤誠 訳
日本評論社(2003)