[課題08] エピサイクロイド

課題

エピサイクロイド

エピサイクロイド(epicycloid)とは，定円の周囲を(接触したまま滑らずに)転がる動円上の1点の軌跡として描かれる曲線です． 動円の半径rと定円の半径Rの比率によって，さまざまな図形が描かれます． その比率が有理数であれば，閉じた曲線となります．

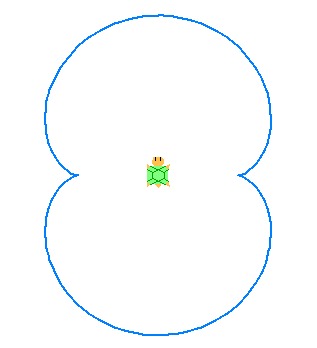
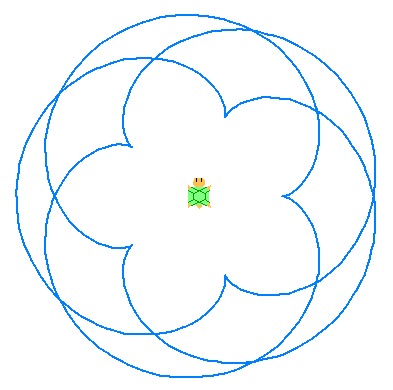
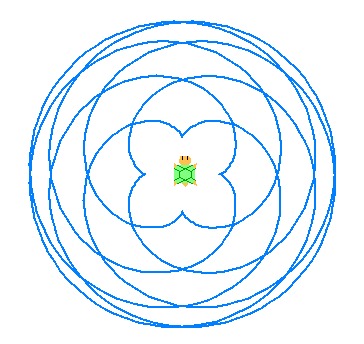
次にエピサイクロイドの例を示します． a,bを正の整数として動円の半径rと定円の半径Rの比をa:bと表しています． なお右端の図にはサイクロイドとともに定円と動円も描いています． また描画過程のアニメーションが示されているページにリンクしています(Epicycloid - Wikipedia)．

a=1,b=2	a=3,b=5	a=7,b=4	a=1,b=3

プログラムではエピサイクロイドの形状を決めるパラメタa,b，大きさを決める動円の半径rはプログラムの最初で適当に定めておいて構いません． プログラムが完成したら，いろいろなパラメタで描けるようにするとよいでしょう．

プログラムテンプレート

次に示すプログラムのテンプレート(雛型)を使って下さい． このプログラムは名前を適宜変えた上で保存して利用してください．

• gtr_template.rb

データ入力の方法

drawメソッドの内部で最初に次のように記述することで3つのパラメタの値を指定できます．

    # a,b,rを取得
    a,b,r = ask('a,b,rの値?').split.map(&:to_i)

プログラムを実行すると，「a,b,rの値?」と質問するポップアップ画面が表示されます． そこで，次のようにa,b,rに代入する値を順に空白で区切って指定して下さい．

 4  7  60

この例の場合，a,b,rには次のように値が代入されることになります．

   a = 4
   b = 7
   r = 60

動円の半径r，定円の半径R(=(b/a)・r)として， エピサイクロイド上の点と中心との距離の最大値はR+2rです(最小値はRです)． この関係とキャンバスサイズからrの適切な値を決めることができるでしょう．

エピサイクロイドのパラメトリック表現

正の整数a,bと動円の半径rが与えられたとき， 定円と動円の接点の極座標系での偏角tをパラメタとして， パラメタtに対するエピサイクロイドの点P_tの位置は次のように表されます．

エピサイクロイドはこのようにパラメトリック曲線として表現されます． n=a/gcd(a,b)として，エピサイクロイドの周期は2nπです(nは整数になります)． つまり動円上の点P_tは周期2nπで最初の位置に戻ります． 課題では1周期分を描画することになります． 今回のプログラムでgcd(最大公約数)を得る方法については以下で示します．

なお上の定義でエピサイクロイドの中心は原点となっていますので注意してください(亀の位置を中心とした式ではありません)． また数学の記法を使って表現しています． プログラムでは三角関数，乗算などはRubyの文法に合わせて記述する必要があります．

エピサイクロイドの描画方法

エピサイクロイド上に点を多数とり，それらの間を(短い)線分でつなぐことでエピサイクロイドを近似的に描画することにします．

具体的には適当な正の整数mを定めて， エピサイクロイドの1周期分のパラメタの区間(0≦t≦2nπ)を 幅δ=2π/mで等間隔に分割します(2nπの区間をmn個に分割します)． それによって得られる(mn+1)個のパラメタの値に対応するエピサイクロイドの点を順に線分でつなぐことにします(注:t=2nπのときの点はt=0のときと同じ点です)．

次の図はa=2,b=3,m=30としたときの例です． 線分で区分的に近似されていることを分かりやすくするためmはわざと小さめにしています． 赤い小円がエピサイクロイド上にとった点を示しています．

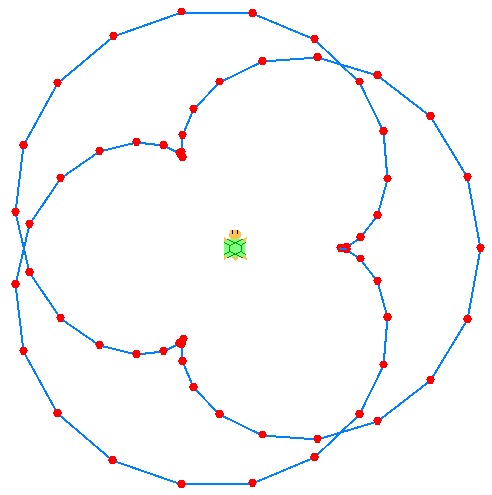
さて亀を中心としてエピサイクロイドを描画するとして， プログラムでの亀の挙動はおおよそ次のようになることを想定しています．

  t = 0のときの点の位置を計算して，その点まで移動(ただし線は描かない)

  t = δのときの点の位置を計算して，その点まで移動
  t = 2δのときの点の位置を計算して，その点まで移動
  t = 3δのときの点の位置を計算して，その点まで移動
    :
    :
  t = mnδ(=2nπ)のときの点の位置を計算して，その点まで移動

  (ただしδ=2π/m)

このように「点の座標を一つ計算してはその点に移動すること」を繰り返していけば，図形を描くことができます． またこのように描画する場合， 次に移動すべき点の位置を描画中に順次計算していくことになり， 描画に用いる点の座標を描画を始める前にすべて計算してしまう必要はないことも分かります．

なお最初の点まで移動するときには線を描かないことに注意してください． また描き終わった後に中心に亀を戻すとすれば，そのときにも線は描かないようにします．

次に参考までにプログラムの冒頭の部分を示します．

  # 周期2nπのnを得る(n = a/gcd(a,b))
  n = a/a.gcd(b) 

  # 分割の個数mの設定(適当な正整数)
  m = 100

  # δ = 2π/m (Math::PI = 円周率π(PI=大文字の「P」と「I」))
  dt = 2*Math::PI/m 

なおmの値は近似の精度に影響します． mの値を大きくするほどデータとしてはよい近似が得られます． ただしある上限を越えるとmを大きくしてもデータとしての点が増えるだけで，描かれる図形は変わらなくなります(画面上に描かれる点の位置の精度に限界があります)．

Tips

除算

整数同士の演算「/」の結果は商であることに注意して下さい．

  a = 1
  b = 2
  c = a/b # c == 0

整数と整数との間で除算を行いたい場合は次のように「to_f」メソッドを利用します．

  a = 1
  b = 2
  c = a.to_f/b # c == 0.5

この例の場合，aに「to_f」メソッドを適用することでaを「1」から「1.0」に変換しています． 「1」と「1.0」ではRuby内部のデータの形式が異なっています(もちろん数値としては同一です)． 「1.0」は整数データではありません． 整数同士でなければ「/」は除算となります．

三角関数，円周率

sin x	Math.sin(x)
cos x	Math.cos(x)
π	Math::PI

なお引数はラジアンで指定します． また円周率の「PI」は大文字の「P」と「I」です．

亀の機能

次のような機能があります．

move(dx,dy)	現在地から横(x方向)にdx，縦(y方向)にdyだけ離れた点に進む．亀の向きに関わらず，キャンバスの座標系を基準とすることに注意せよ．	move(60,-30)
moveto(x,y)	点(x,y)に移動する．ここで指定する値については「画面の座標系」を参照のこと．	moveto(0,0)
mark	現在の位置と向きを記憶する．後でbackすると記憶した位置に戻ることができる(向きも戻る)．
back	markした場所に戻る．そのときの方位を向く(戻ったら，その場所についての記憶はなくなる)． hoverに組み込めば線を描かずにmarkした状態に戻れる．
pos	亀の現在位置(x,y)を得る	x,y = pos()
set_speed(MAX_SPEED)	亀の速さを最大にする

プログラムにインデントをつける

プログラムには適宜インデントをつけるようにしてください(各行の先頭に適宜空白を入れる)． Emacsでは[TAB]によって，いつでも適宜インデントを入れることができます(前の行に対して相対的に)．
メソッド定義やブロック等のプログラムの構造において， それらの内部ではインデントを一律に(少し)深くすることで， プログラムを見たときに構造を分かりやすくすることができます． またそうすることでプログラムに構造上の間違いがあったときにも，それを見つけやすくすることができます．

プログラムの挙動を調べる方法

プログラムの作成中にはプログラムが期待通りに動かないことがよくあります． そのようなときにプログラムの記述を調べるだけではなく， 動作中の挙動を調べれば間違いを発見しやすくなることが少なくありません．
具体的には変数の値を調べることがポイントです． 変数がどんな値になっているか，それが期待通りかどうかを調べることで， プログラムの挙動を把握しやすくなるでしょう．
そのような場合Rubyではpメソッドを使うと便利です．

  p [a,b,r]  # 変数a,b,rの値を表示する(a,b,rは定義済みとする)

挙動をチェックしたいところに上のような行を(一時的に)入れてみてプログラムを実行すると，端末の画面上に値が表示されるでしょう(その行が実行されれば)． その結果を参考にしてみて下さい． なお「p」の後にスペースを入れることに注意してください(そうしないと解釈が変わってしまいます)．

サンプルプログラム

繰り返し処理のサンプルを示します．

• sin_curve.rb
• stars5.rb

これらをブラウザの画面で開いたときに文字化けしてしまう場合には， ダウンロードしてEmacs等で開いてみて下さい．