[課題15] パスカルの三角形

課題

以下の説明にしたがって，タートルグラフィクスでパスカルの三角形に基づいた図形を描画するプログラムを作成して下さい．

パスカルの三角形はある規則にしたがって正の整数を三角形に並べたものです．各横列をまとめて，上から順に第0段，第1段，第2段のように呼ぶことにします．第k段は(k+1)個の整数で構成されています．

この課題では，パスカルの三角形の各要素を配列を活用して計算して，パスカルの三角形の第0段から第n段目までの各要素を正方形で表現して，与えられた条件にしたがって各正方形の色を塗り分けることで図形を描画するようにします．

具体的には二つの整数n,mを指定して(nは0以上,mは2以上)，パスカルの三角形の第0段から第n段までについて，mの倍数に対応する正方形とそれ以外の数に対応する正方形を異なる2色で塗り分けるようにします．なお正方形には枠をつけることにします．

n,mの値は変数で指定して，適宜変えられるようにしておいてください．実行中にn,mの値をask("...")で取得するか，コマンドライン引数で指定できるようにするとよいでしょう． askを使う場合には例えば次のように記述します(コマンドライン引数の場合はこのページの末尾を参照して下さい)．


  n = ask("第何段目まで(n)?").to_i
  m = ask("何の倍数を塗り分ける(m)?").to_i

描画する正方形の大きさ，2つの色，枠の色は自由に決めてください．プログラムが完成したら，大きめのnを指定して，さまざまなmについて結果を見てみるとよいでしょう．

パスカルの三角形

パスカルの三角形は正の整数を三角形に並べたものです．各横列をまとめて，上から順に第0段，第1段，第2段のように呼ぶことにします．それらの整数は次のように決められています．

左右の端の数＝1
それ以外の要素＝左上の数＋右上の数

左の図はパスカルの三角形の第0段から第6段までを示したものです．三角形はいくらでも下向きに伸ばしていくことができます．

パスカルの三角形の構成法から，三角形の第0段から順に各段の各要素の値を計算できることが分かるでしょう．まず第0段の要素は1個で1と決まっています．第k段(k≧1)については，第(k-1)段の要素から計算できます．まず両端は1と決まります．両端以外は第(k-1)段の数から計算できます．具体的には第k段の左端の要素から順に0,1,2,...,kと番号を割り当てたとして， i番(i=1,2,...k-1)の要素は(k-1)段の(i-1)番の要素とi番の要素の和です．


  [第k段の0番の数] ＝ [第k段のk番の数] ＝ 1
  [第k段のi番の数] ＝ [第(k-1)段の(i-1)番の数] ＋ [第(k-1)段のi番の数] (i=1,2,...,k-1)

つまり第(k-1)段の要素がデータとして配列に格納されていたら，そこから第k段の要素の配列を得ることができるわけです．第0段から第8段までの値を配列の形式で示すと次のようになります．


  0 [1]
  1 [1, 1]
  2 [1, 2, 1]
  3 [1, 3, 3, 1]
  4 [1, 4, 6, 4, 1]
  5 [1, 5, 10, 10, 5, 1]
  6 [1, 6, 15, 20, 15, 6, 1]
  7 [1, 7, 21, 35, 35, 21, 7, 1]
  8 [1, 8, 28, 56, 70, 56, 28, 8, 1]

パスカルの三角形の塗り分け


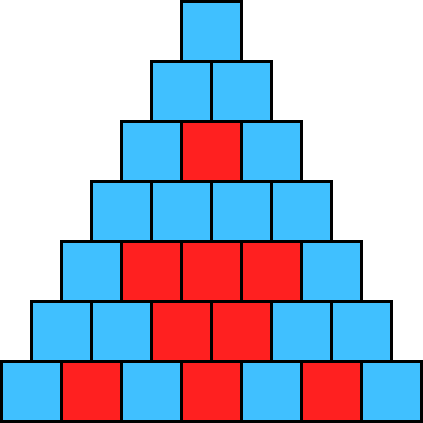
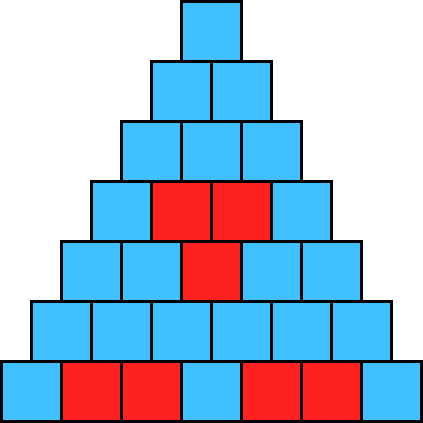
n=6, m=2	n=6, m=3

今回の課題ではパスカルの三角形の第0段から第n段までの要素のうち，mの倍数に対応する正方形とそれ以外の数に対応する正方形を異なる2色で塗り分けるようにします(正方形には枠を付けます)．左にn=6,m=2の場合とn=6,m=3の場合の図を示します．

二つの色を表す定数を次のように用意して使うとよいでしょう．


class Turtle

  COLOR0=[255,0,0] # mの倍数の要素の色(赤)
  COLOR1=[0,0,255] # それ以外の要素の色(青)

  def draw

　　     :
　　     :
     set_color(COLOR0)
　　     :
　　     :
     set_color(COLOR1)
　　     :
　　     :

     
  end
  
end

なお正の整数a,bについて，aがbの倍数かどうかは，授業でこれまでに紹介している基本的な算術演算で判定可能です(考えてみて下さい)．

パスカルの三角形の計算と描画について

パスカルの三角形の描画に使われる要素をすべて計算してしまってから三角形を描画してもよいでしょうし，上から順に一段ずつ計算しつつ，その都度描画してもよいでしょう．余裕があれば，各段の要素が左右対称になっていることを利用して，計算処理の回数と保存するデータの量を減らすように工夫してみて下さい．

パスカルの三角形の描画に使われる要素を事前にすべて計算する場合，三角形のデータは2次元配列(配列の配列)に配置するとよいでしょう．たとえばpascalという配列を適宜準備したとして， pascal[j][i]が上からj段目の左からi番目(ただしi=0,1,2,...,j=0,1,2,...) の要素の値となるように処理します．

2次元配列の生成と処理については以下で説明しています．

プログラムテンプレート

次に示すプログラムのテンプレート(雛型)を適宜名前を変えて使って下さい．

gtr_template.rb

配列，2次元配列(配列の配列)の生成と処理

配列を生成して，同時に要素の値を初期化(設定)する方法を示します．すべての要素を同一の値で初期化することもできますし，ブロックを使うことで要素ごとに個別に値を初期化することもできます．


  n = 5

  # n個の要素の配列を生成する．全ての要素を「true」にする．
  x = Array.new(n,true) # x == [true,true,true,true,true]
  
  # n+1個の要素の配列を生成する．全ての要素を「0」にする．
  y = Array.new(n+1,0) # y == [0,0,0,0,0,0]
  
  # n個の要素の配列を生成する．i番目の要素の値を「i+1」に設定する
  z = Array.new(n) { |i| i+1 } # z == [1,2,3,4,5]

配列において，各要素の値を他の要素の値を使って設定する例を示します．


  n = 5

  # n個の要素の配列を生成する．全ての要素を「0」にする．
  x = Array.new(n,0) 

  x[0] = 1
  (n-1).times do |i| # i = 0,1,...,n-2
    x[i+1] = 2*x[i]
  end

  # この時点で次のようになっている．
  # x ==> [1,2,4,8,16]

次に2次元配列(配列を要素とする配列)を生成して，要素ごとに値を設定する例を示します．


  m,n = 2,3 # m = 2; n = 3

  #
  # ary[j][i] (0 <= j < m, 0 <= i < n)を生成する
  # (「n要素の配列」がm個並んだ配列を作る)
  # 要素の値はすべて0で初期化する．
  #
  ary = Array.new(m) { Array.new(n,0) }

  # この時点で次のようになっている．
  # ary ==> [[0,0,0],[0,0,0]]
  
  m.times do |j|
    n.times do |i|
      ary[j][i] = j*n + i
    end
  end

  # この時点で次のようになっている．
  # ary ==> [[0,1,2],[3,4,5]]

  # [注意]
  # 文法上は次のように初期化することもできる．
  # しかし上の場合とは異なる状態になる．
  # (一つの「n要素の配列」がm回繰り返し参照されている配列を作る)
  #
  foo = Array.new(m,Array.new(n,0))

  # この時点で次のようになっている．
  # foo ==> [[0,0,0],[0,0,0]]

  m.times do |j|
    n.times do |i|
      foo[j][i] = j*n + i
    end
  end

  # この時点で次のようになっている．
  # foo ==> [[3,4,5],[3,4,5]]

なおこの課題で作成するプログラムでは，このような2次元配列を使わなければならないわけではありません．

times，upto，downtoメソッド

timesに似た繰り返しのためのメソッドとしてupto/downtoがあります． upto/downtoの処理はtimesでも記述可能ですが，upto/downtoを使うことによって，記述をシンプルにできます．

  # i = a,a+1,...,b-1,bについて，ブロック(do...end)の処理を繰り返す
  a.upto(b) do |i|


  end

なお「a > b」の場合もエラーにはなりません．その場合は何もしないで処理を終了します．

downtoはuptoの逆順に繰り返します．

  # i = b,b-1,...,a+1,aについて，ブロック(do...end)の処理を繰り返す
  b.downto(a) do |i|

  end

uptoと同じく「b < a」の場合もエラーにはなりません．その場合は何もしないで処理を終了します．

同様の仕様として，timesの繰り返し回数が0以下の場合，何もしないで終了します．

何もしないことに意味があるかと思うかもしれませんが，このような仕様を活かすことで，例外処理を不要にできる場合があります．

サンプルプログラム

2次元配列(配列を要素とする配列)を生成して，要素ごとに値を設定して処理するプログラムの例を示します．

9x9.rb(2次元配列の扱いの例)

[参考] コマンドライン引数の扱い

コマンドライン引数(配列ARGV)をタートルグラフィクスで扱うには， push,retrieveを使います．

push(x)
データxを亀に記憶させる．いくつでも記憶させられる．
y = retrieve( )
記憶させたデータを引き出す． 2つ以上のデータを記憶させている場合，記憶させた順番で取り出される．取り出したデータは亀の記憶からなくなる．

次に例を示します．


  class Turtle
    def draw

      # 亀に記憶させたデータを取り出して，aに代入する
      a = retrieve() 

      # 亀に記憶させたデータを取り出して，bに代入する
      b = retrieve()
  
    end
  end

  # コマンドライン引数を一つ取り出して，整数に変換する
  m = ARGV.shift.to_i

  # コマンドライン引数を一つ取り出して，整数に変換する
  k = ARGV.shift.to_i

  # 亀を準備
  t = Turtle.new()

  
  t.push(m) # 亀にmの値を記憶させる
  t.push(k) # 亀にkの値を記憶させる

これを次のように実行したとします(ファイル名をarg.rbとする)．


  $ ruby arg.rb 50 3

このときdraw内のretrieve()でa=50,b=3と代入されます．