[課題22] マージソート

課題

マージソートとよばれるアルゴリズム(処理手順)で数値の配列の要素を小さい順に並べ替えた配列を作るメソッドを作成してください．またそのメソッドをテストするプログラムを以下に示すように作成して，完成したプログラムを提出してください．

一般にデータの間に順序を定めて，それに従って一連のデータを並び替える処理をソートと呼びます．典型例として次のように整数を昇順に並べることが挙げられます．


  ソート前: 37 86 54  2 19 60  7 51 28
  ソート後:  2  7 19 28 37 51 54 60 86

ソートにはさまざまな実現方法が知られています．ここではマージソートという方法を用いることにします．マージソートのアルゴリズム(処理手順)については以下で詳しく説明します．

テストプログラム(テンプレート)

今回のプログラムは次のテンプレートにしたがって作成してください．

merge_sort_template.rb

このテンプレートのメソッドmerge_sortを課題として作成して下さい．

このプログラムでは，最初に予め定義してある配列についてmerge_sortを実行するようになっています．さらに結果として得られた配列が正しくソートできているかどうかを確認して，ソートできていた場合には「OK」，そうでない場合には「FAILED」と表示して終了します．


  $ ruby merge_sort.rb
  input:  56 39 18 64 41 46 94 43 39 1
  output: 1 18 39 39 41 43 46 56 64 94
  OK

merge_sortメソッドが完成したら，プログラムの「__END__」の行を削除して(あるいはコメントにして)実行してみて下さい．そのように変更した場合にはテストをR回(R=100)繰り返し実行するようになっています．テストでは長さN(=32)の非負整数の配列をランダムに生成してmerge_sortで処理します．つづいて，merge_sortの結果として得られた配列がソート済みかどうかを確認して，ソートができていない場合はエラーで終了します． R回のテストですべてソートができていた場合にはOKと表示して終了します．


  $ ruby merge_sort.rb
  input:  33 36 38 58 49 59 15 30 20 70 85 33 25 50 79 62 79 54 48 60 71 59 7 7 47 20 81 95 75 42 8 12
  output: 7 7 8 12 15 20 20 25 30 33 33 36 38 42 47 48 49 50 54 58 59 59 60 62 70 71 75 79 79 81 85 95

   :
   :

  input:  63 1 35 99 31 48 36 71 42 3 50 9 34 41 4 97 87 92 76 62 83 18 79 49 96 86 92 95 75 32 13 67
  output: 1 3 4 9 13 18 31 32 34 35 36 41 42 48 49 50 62 63 67 71 75 76 79 83 86 87 92 92 95 96 97 99
  OK

Rubyではプログラムに「__END__」という行があると，そこまででプログラムの解釈を終了して，その後の行は一切処理しません．ちなみに「__END__」より下の行をプログラムで「データ」として使う仕組みも提供されています．

マージソートのメソッド

今回作成するマージソートのメソッドは次のような仕様で定義します．数値の配列を引数として，結果として昇順にソートされた配列を返すことにします．


  # マージソート
  # a: ソートする配列
  def merge_sort(a)
    
  end


  # ソートする配列
  ary = [4,2,5,1,3] 

  # aryをソートして，ソートされた結果をs_aryに代入する
  # s_ary == [1,2,3,4,5]が期待される
  # (マージソートは「配列」を値とするメソッド)
  s_ary = merge_sort(ary)

以下で示す通り，このメソッドmerge_sortは再帰呼び出しで実現します．次のことに注意してください．

基本的に「メソッドで最後に評価した値」がメソッドの値となる
if式では「if式内で最後に評価した値」がif式の値となる

また上で示したようにメソッドmerge_sortは配列を値とすることを想定しています． Rubyでは配列をメソッドの値とすることもできます．次に簡単な例を示します．


  def f(x) # xは整数を仮定
    if x.even?
      y = x*x  
      [x,y]
    else
      y = 2*x
      z = 3*x
      [z,y,x]
    end
  end

  a0 = f(2) # a0 == [2,4]
  a1 = f(3) # a1 == [9,6,3]

マージソートのアルゴリズム

マージソートは再帰的にソートを行う方法の一つです．基本的な考え方は配列全体を前半と後半に分割して，それぞれを再帰的にソートして，それらの結果を適宜まとめて全体をソートするというものです．再帰的に分割していって，要素数が2以下になれば再帰的に処理しなくても簡単にソートできます．具体的には次のようにしてソートします．ここでは配列aをソートするものとします．

配列aの要素数が1以下(0か1)であれば，ソートした結果は配列aそのものである．

配列aの要素数が2であれば，ソートした結果は次の通りとなる．

a[0] <= a[1]のときは配列aそのもの
そうではないときは[a[1],a[0]]という配列(2つの要素を入れ替えた配列)

配列aの要素数が3以上のとき(上のどちらのケースでもないとき)は次のようにソートする

配列aの前半をソートした結果をa1とする(再帰的処理)
配列aの後半をソートした結果をa2とする(再帰的処理)
得られた配列a1と配列a2をマージする(まとめる)．マージした結果が配列a全体をソートしたものになる．

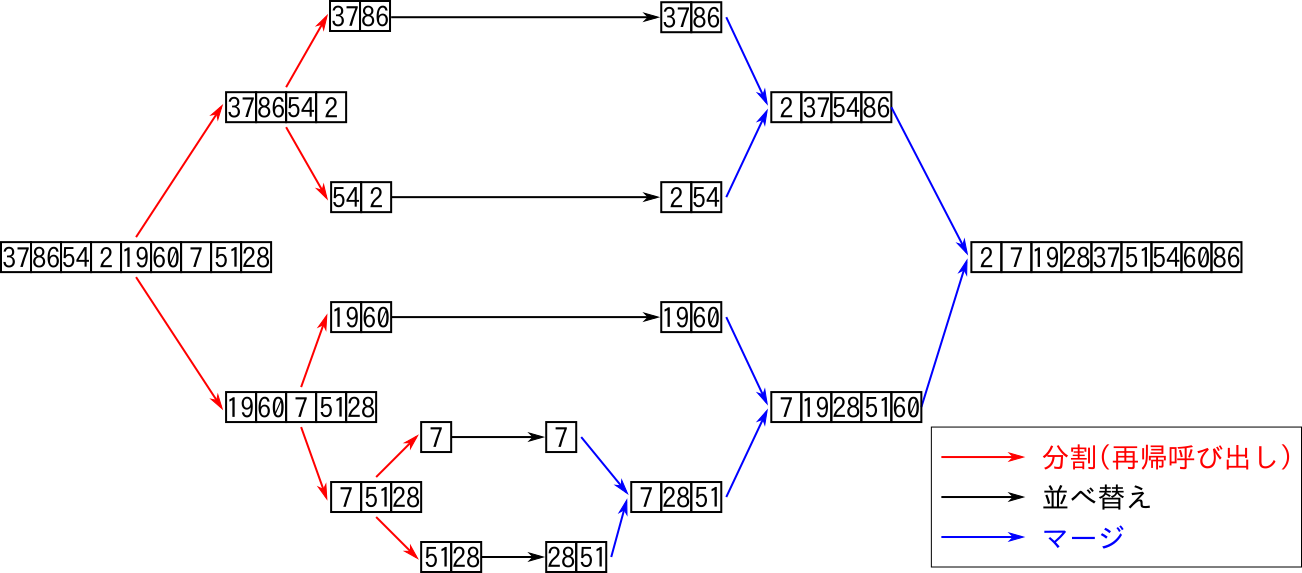
ソートされた配列が二つあるときに，それらを全体としてソートされた一つの配列にまとめる処理をマージ(merge)と呼びます．ソートされた二つの配列の先頭から順に適切に要素を取り出して，取り出した要素を別途用意した空の配列に順に並べていくことでマージを実現できます．

具体例を示します．配列a=[3,5,8,11]と配列b=[1,4,10,15,20]があったとき，それらをマージした配列cは次のようにして得られます．

配列a	配列b	配列c	実行する処理
[3,5,8,11]	[1,4,10,15,20]	[ ]	3,1を比較→配列bから1を取り出して配列cへ
[3,5,8,11]	[4,10,15,20]	[1]	3,4を比較→配列aから3を取り出して配列cへ
[5,8,11]	[4,10,15,20]	[1,3]	5,4を比較→配列bから4を取り出して配列cへ
[5,8,11]	[10,15,20]	[1,3,4]	5,10を比較→配列aから5を取り出して配列cへ
[8,11]	[10,15,20]	[1,3,4,5]	8,10を比較→配列aから8を取り出して配列cへ
[11]	[10,15,20]	[1,3,4,5,8]	11,10を比較→配列bから10を取り出して配列cへ
[11]	[15,20]	[1,3,4,5,8,10]	11,15を比較→配列aから11を取り出して配列cへ
[ ]	[15,20]	[1,3,4,5,8,10,11]	配列aが空→配列bの要素をすべて順番に配列cに取り込む
		[1,3,4,5,8,10,11,15,20]	マージ終了

この例で示した通り，マージする配列のうちの一方が空であれば，もう一方の配列に残っている要素は一度に取り込むことができます． Rubyではこの処理は配列の連結で実現できます．なお空の配列を連結することも許されます．空の配列を連結しても配列は何も変わりませんが，そのような場合も含めて考えることでプログラムを単純にできます．


   a = [1,2,3]
   b = [4,5]
   c = a + b  # c == [1,2,3,4,5] (a==[1,2,3], b==[4,5])

   d = [ ]
   c = c + d  # c == [1,2,3,4,5] (d==[ ])

アルゴリズムに関する補足

上に示したアルゴリズムでは要素数＝2のときも場合分けして処理していますが，この場合でも再帰的に処理することができます(再帰呼び出しで要素数＝1の場合に帰着されます)．その方がアルゴリズムの記述は簡単になります．しかし要素数＝2のときは簡単にソートできますので，上のアルゴリズムではわざわざ再帰呼び出しはしないようにしています．

また上に示したアルゴリズムでは要素数＝0の場合も考えています．このケースは空の配列が引数としてメソッドに渡されるとき以外は発生しません．しかしこのケースも処理しないと，空の配列が渡されたときに困ったことになります．

サンプルプログラム

再帰呼び出しのプログラムのサンプルを示します．プログラムをブラウザの画面で開いたときに文字化けしてしまう場合には，ダウンロードしてEmacs等で開いてみて下さい．

サンプルプログラム(再帰的な処理)

技術要素

いかに配列のメソッドを紹介します．必ずしもすべてのメソッドを使わなくても構いません．

配列の要素数を得る(size)
sizeメソッドで配列の要素数が得られる．


  a = [8,1,25,6]
  y = a.size # y == 4

  b = ['x',[0,1],true]
  z = b.size # z == 3

部分配列
配列の一部を取り出すことができる．


  # 配列aについてa[i0..i1]でi0番めからi1番めまでの要素からなる配列を作る
  a = [8,1,25,6,3,0]

  a0 = a[0..1]  # a0 == [8,1]
  a1 = a[0..2]  # a1 == [8,1,25]
  a2 = a[1..2]  # a2 == [1,25]
  a3 = a[1..3]  # a3 == [1,25,6]
  a4 = a[2..-1] # a4 == [25,6,3,0] (a[2]..末尾まで)
  a5 = a[1..-2] # a5 == [1,25,6,3] (a[1]..後ろから2番めまで)

なお例に示したように添字に負の整数を指定すると末尾から要素を数えることができる．

配列が空かどうかを判定する(empty?)


  # 空の配列を準備する
  ary = []

  ary.empty? # ==> true (aryは空である)

  ary = [2,3,5] 
  
  ary.empty? # ==> false (aryは空ではない)

配列から先頭の要素を取り出す(shift)
shiftメソッドで配列から先頭の要素を取り出せる．取り出した先頭の要素は配列から削除される．結果として，他の要素は一つずつ前にずれることになる．
```
  a = [2,3,4,5,6]
  len = a.size # len == 5

  b = a.shift # ==> b == 2, a == [3,4,5,6]
  len2 = a.size # len2 == 4  (先頭が取り除かれた→要素が1個減った)
```

配列の末尾に要素を追加する(push)
pushメソッドで配列の末尾に要素を追加できる．


  a = []
  a.push(2) # ==> a == [2]
  a.push(3) # ==> a == [2,3]
  a.push(5) # ==> a == [2,3,5]

配列を連結する(+)
+演算子によって，配列同士を結合した配列を生成できる．


   a = [1,2,3]
   b = [4,5]
   c = a + b  # c == [1,2,3,4,5]

   d = [1,1,0]
   c = c + d  # c == [1,2,3,4,5,1,1,0]

要素を逆順に並べた配列を作る(reverse)
reverseメソッドで要素を逆順に並べた配列を生成できる．
```
  a = [8,1,25,6]
  b = a.reverse  # b == [6,25,1,8], a == [8,1,25,6]
```

要素をコピーした配列を作る(dup)
dupメソッドで各要素をコピーした配列を作ることができる．


  a = [1,2,3,4]
  b = a         # bはaと同じ配列を参照
  c = a.dup     # cはaの配列の複製

  # cの要素を書き換えても，a,bは影響を受けない(cとa,bは別々の配列を参照している)  
  c[0] = 0 # a == [1,2,3,4], b == [1,2,3,4], c == [0,2,3,4]

  # bの要素を書き換える→aの要素も書き換わる(a,bは同じ配列を参照している)  
  b[0] = 5 # a == [5,2,3,4], b == [5,2,3,4], c == [0,2,3,4]

[補足] 厳密にはdupは各要素への参照をコピーするだけです(shallow copy)．要素自体をコピーするには別の方法が必要です(今回dupメソッドを使うとしても，このことを気にする必要はないはずです)．


  a = [1,[2,3],4]
  b = a.dup

  b[0] = 0    # a == [1,[2,3],4], b == [0,[2,3],4]
  b[1][0] = 0 # a == [1,[0,3],4], b == [0,[0,3],4]

[参考] ソートのアルゴリズムの効率

ソートを実現する方法(アルゴリズム)はいろいろ考えられます． (正しく処理を行う)どんな方法でもソートした結果は基本的に同じです(厳密には同順位となる要素をどう並べるかという点で相違がありえます)．それではどんな方法を使っても同じことかと言えば，決してそうではありません．アルゴリズムによってソートにかかる手間は異なります．つまり処理の効率が異なります．ソートにかかる「手間」とは，データの比較あるいは移動(コピー)といった処理で，処理回数が少ないほど効率がよいと評価できます(評価の観点としては処理の過程で必要となるデータを保存するスペースの広さも考えられます)．要素の個数が少ない場合にはどんな方法でも実質的な差はありませんが，要素が多くなるにしたがって，効率の差が大きく影響するようになります．

ソートのアルゴリズムの例として，バブルソートと呼ばれるものがあります．これは「隣同士を比較して前の要素が大きいなら2つを交換する」ことを基本とするアルゴリズムです．「配列の先頭から順に基本操作を繰り返すこと」を必要なだけ繰り返すことで全体をソートできます．次のbubble_sort!にそのプログラムを示します．プログラムとしてはとても単純です．


def bubble_sort!(ary)
  n = ary.size - 1
  j = 0
  sorted = false
  while j < n and (not sorted)
    sorted = true
    (n-j).times do |i|
      if ary[i] > ary[i+1]
        ary[i+1],ary[i] = ary[i],ary[i+1]
        sorted = false
      end
    end
    j += 1
  end
  ary
end

ここで今回の課題のマージソートとバブルソートの数値データの比較回数を調べてみます．ソートするデータによって比較回数は変動しますが，ソートする数値がN個として，バブルソートでの比較回数はおおよそN(N-1)/2回程度，マージソートの場合はおおよそN・log₂N回程度です．

いくつかのNについてN(N-1)/2回とN・log₂N回を計算して比較してみると，次のようになります(後者は四捨五入しています)．

データの個数による「比較処理の回数」の見積もり
N	100	1000	10000	100000	1000000
N(N-1)/2	4950	499500	49995000	4999950000	499999500000
N・log₂N	664	9966	132877	1660964	19931569

Nが大きくなるにつれ，「比較回数」の差がどんどん大きくなっていくのが見て取れます．

実験として，いくつかのNについてランダムに配列を生成して，それを二つのアルゴリズムで別々にソートしたときの処理時間(秒)を比較してみたところ次のような結果が得られました．

データの個数による処理時間の比較(単位:秒)
N	1000	10000	50000	100000
マージソート	0.00	0.03	0.16	0.33
バブルソート	0.06	5.85	139.01	557.94

アルゴリズム次第で処理効率に大きな差が現れることが実感できるのではないかと思います(注:マージソートでN=1000のときは小数点以下第3位を四捨五入して0.00になっています)．