[課題25] 二分法

課題

二分法に基づいて，指定された1変数多項式の根(の近似値)を指定された区間内で一つ求めるメソッドを作成してください．また同じファイルで適当な多項式について実際に根(の近似値)を求めるようなプログラムを作成し，プログラムを提出してください．

対象とする多項式はProcとしてメソッドの引数に与えるようにします．次のように式を直接書き下して構いません．


  f = proc { |x| 4*x**3 - 7*x**2 - 36*x + 63 } # 4x³ - 7x² - 36x + 63

できれば多項式の係数列(各次数の係数を並べた配列)から多項式の値を計算するProcを生成するメソッドを別途定義して利用できるようにしてみてください．


  g = polynomial(1,-3,-4,12) # x³ - 3x² - 4x + 12 (多項式生成メソッドを定義して利用する例)

さらに余裕があれば，以下に示すようにsin関数の多項式展開に基づいて， sin(x)=0を満たす解としてπの近似値を求めてみてください(3 < π < 4を仮定して構いません)．

二分法

ここでは実数上の連続関数f(x)についてf(x)の根(の近似値)を求める手法として二分法を紹介します．中間値の定理を使うとf(x)について次が成り立つことが分かります．


a < bとして，f(a)・f(b) < 0のとき，区間(a,b)内にf(c)=0を満たすcが存在する．

そこで条件を満たす区間(a,b)があれば，次のようにしてf(x)=0を満たすx(の近似値)を一つ求めることができます．

aとbを指定する(f(a)・f(b) < 0, a<bとする)．

m = (a+b)/2とする．

(a,b)の区間幅が十分狭い(b-a<ε)，あるいはf(m)=0のときはステップ5に進む．そうでないときは次のステップに進む．

f(a)・f(m) < 0であれば，b = mとする(区間の前半を選ぶ)．そうでなければ，a = mとする(区間の後半を選ぶ)．

ステップ1に戻る．

x=mを根(の近似値)とする．

(a,b)の中点をmとしてf(m)の値を使って根の存在する範囲を狭めていくのが二分法の基本戦略です．処理が繰り返される間は，常にf(a)・f(b) < 0を満たすように区間が更新されますので，(a,b)内に根が一つは含まれることになります．また処理を繰り返すたびにaかbが更新されて，区間(a,b)の幅は半分ずつになっていきますので，いつかは区間幅が十分狭くなり(b-a<ε)，x=mが近似値として得られます．あるいは区間幅が十分狭くなくても，たまたまf(m)=0となってx=mが見つかる場合もありえます．

二分法のメソッド

作成する二分法のメソッドは，例外的なケースも扱うことにして，次のように定義することにします．

なお「a < b」であることは仮定してよいことにします．そうでない場合も扱えるようにすることも，もちろん考えられます．

f(a)・f(b)<0のとき
区間(a,b)内の根(の近似値)の一つを返す．

f(a)・f(b)=0のとき
c∈{a,b}のうちf(c)=0を満たすものを一つ返す(c=aかc=b，f(a)=f(b)=0のときはどちらか一方を選んで返す)．

f(a)・f(b)>0のとき
(区間(a,b)内の根の有無に関わらず)nilを返す．


  # 二分法メソッド
  # f: 多項式f(x)を表すProc
  # a,b: 区間の両端点(a < bを仮定してよい)
  # eps: b-a<epsのときに区間幅が十分狭いとみなすことにする
  # 
  def bisection(f,a,b,eps)

  end

  EPS=1e-15 # EPS=10^-15
  # f(x) = 4x³ - 7x² - 36x + 63 = (x+3)(x-3)(4x-7) 
  f = proc { |x| 4*x**3 - 7*x**2 - 36*x + 63 } 
  x0 = bisection(f,-1,2,EPS) 
  x1 = bisection(f,4,8,EPS)  # x1 == nil (二分法の前提を満たさない)

  # g(x) = x³ - 3x² - 4x + 12 = (x+2)(x-2)(x-3) (多項式生成メソッドを定義して利用する例; 可変個の引数のメソッドとして定義)
  g = polynomial(1,-3,-4,12)  
  x2 = bisection(g,-4,5,EPS) 

  # h(x) = 2x² - 9x - 5 = (2x+1)(x-5) (多項式生成メソッドを定義して利用する例; 可変個の引数のメソッドとして定義)
  h = polynomial(2,-9,-5)   
  x3 = bisection(h,-3,3,EPS)

補足

コンピュータでの一般的な数値データ形式での精度の限界から区間幅のパラメタepsはいくらでも小さく設定できるわけではありません．このとき根の大きさも影響します．また一般には精度の限界から計算誤差が生じます．今回の課題ではこのような問題についてはとくに考慮しないことにします．

次に示すコードをプログラムの先頭にコピーして入れておくようにして下さい(必要事項は記入して下さい)．


=begin

所属:     
氏名:     
学生番号:
難易度(5段階評価): 

感想など(任意)

=end

Tips

プログラム作成に参考となるであろう技術要素を以下に示します．

絶対値が小さな数の表現
小さな数を指数形式で与えることができます．
```
  # 「10^-14」を表す
  1e-14
```

絶対値abs
absメソッドで数値(整数，実数)の絶対値が得られます．


  c = -1.234
  c.abs # ==> 1.234
  
  a = 3
  b = 2.5
  (a-b).abs # ==> 0.5

無限ループloop
loopにブロックを与えることで無条件での繰り返し処理(無限ループ)を実行できます． loopでは通常ブロック内部で条件を定めて内部から脱出するようにします．ブロックからの脱出には「break」や「return」が使えます．
次に例を示します． returnによって値を返すことでメソッドを終了させています(loopからも脱出します)．
```
  # x以外で0 ≦ y ＜ nを満たす整数yをランダムに返す
  def foo(x,n)
    loop do 

      # 0 ≦ y ＜ nを満たす整数yをランダムに生成する
      y = rand(n)

      # returnで常にメソッドの実行を終了して，値を返す．
      # (x ≠ yならreturnでyをメソッドの値として返す)
      return y if x != y

    end
  end  

  a = foo(5,10)
```
このメソッドは次のようにも定義できます． breakによってloopから脱出したら， loopの後の処理を続けます．
```
  # x以外で0 ≦ y ＜ nを満たす整数yをランダムに返す
  def foo(x,n)
    y = nil  # [*注意*] この行も必要
    loop do 

      # 0 ≦ y ＜ nを満たす整数yをランダムに生成する
      y = rand(n)

      # breakで繰り返しを中断できる．
      # (x ≠ yならループから抜ける)
      break unless x == y

    end
    y # yをメソッドの値として返す
  end  

  a = foo(5,10)
```
この例で，最初に「y = nil」としているのは変数の有効範囲(scope)の問題を回避するためです．ブロック(do...end)内で新たに出現した変数はブロック内部のみで有効な変数になります．そこで最初の「y = nil」がないとすると，変数yがブロック内部での変数となってしまって，メソッドの末尾の「y」が未定義になってしまいます．ブロックに入る前に「y」を定義しておけば，この問題はを回避できます．なおこの場合，最初に「y」に代入する値は何でも構いません(loop内で書き換えられるため)．

なお今回の課題では必ずしも無限ループを使う必要はありません(もちろん使っても構いません)．

サンプルプログラム

次のページにサンプルプログラムを示します．プログラムをブラウザの画面で開いたときに文字化けしてしまう場合には，ダウンロードしてEmacs等で開いてみて下さい．

手続き(サンプルコード)

(参考)多項式の生成

n次多項式f(x)は次のように与えられます．

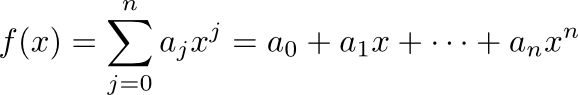
このような多項式を表すProcを次のようなメソッドで生成することが考えられます．


   # polynomial_ascend: 多項式生成メソッド(1)
   # a_jをx^jの係数とするn次多項式f(x)を表すProcを生成する
   # 係数の列が次のように配列として渡されるものとする
   # (低次の項から並んでいるものとする)
   # c=[a₀,a₁,...,a_n]
   def polynomial_ascend(c)

   end

   ### 多項式生成の例(低次から並べる場合)

   # f(x)= 2 - 3x + x²の係数を表す配列
   c_f = [2,-3,1] 

   # この例ではfが「x² - 3x + 2」を計算するProcとなることが期待される
   f = polynomial_ascend(c_f) 

   # y = f(1) 
   # (f(x) = x² - 3x + 2)
   y = f.call(1)  # y == 0

   # z = f(3/2)
   # (f(x) = x² - 3x + 2)
   z = f.call(1.5)  # z == -0.25

   # polynomial_descend: 多項式生成メソッド(2)
   # a_jをx^jの係数とするn次多項式f(x)を表すProcを生成する
   # 係数の列が次のように配列として渡されるものとする
   # (高次の項から並んでいるものとする)
   # c=[a_n,a_n-1,...,a₀]
   def polynomial_descend(c)

   end

   # 多項式生成の例(高次から並べる場合)

   # g(x)=x³ - 3x² - 4x + 12の係数を表す配列
   c_g = [1,-3,-4,12]

   # この例ではgが「x³ - 3x² - 4x + 12」を計算するProcとなることが期待される
   g = polynomial_descend(c_g) 

   # y = g(1) 
   # (g(x) = x³ - 3x² - 4x + 12)
   y = g.call(1)  # y == 6

   # y = g(3/2) 
   # (g(x) = x³ - 3x² - 4x + 12)
   y = g.call(1.5) # y == 2.625

(参考) 可変個の引数をとるメソッドの定義

メソッドの引数に次のように「*」をつけて定義することで，可変個の引数をまとめて配列として受け取ることができます．


  # 1個以上の引数をとるメソッド
  # cは必須，残りをまとめて配列aとして受け取る
  def scale(c,*a)
    # aの各要素にブロックの処理を適用した結果の配列を生成する
    a.map { |x| c*x } 
  end

  y = scale(2,1,3,5) # y == [2,6,10] (c=2,a=[1,3,5]となる)
  z = scale(-3,5,4)  # z == [-15,-12] (c=-3,a=[5,4]となる)
  w = scale(4)       # w == [] (c=4,a=[]となる)

  # 0個以上の引数をとるメソッド
  # 引数をすべてまとめて配列aryとして受け取る(0個でもOK)
  def argc(*ary)
    ary.size
  end

  n = argc(:this,1,"test") # n == 3 (ary == [:this,1,"test"]となる)
  m = argc() # m == 0 (ary == []となる;つまり空の配列)

(参考) sin関数の多項式近似

sin関数は次のように多項式に展開されることが知られています．

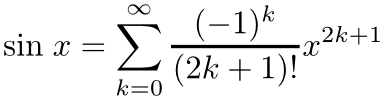
nを適当に定めて，この展開式の第n項までの多項式によって， sin関数の近似を得ることができます．第n項までの多項式の係数列を配列として適宜生成した後，それをpolynomialメソッドに渡すことで， sin関数を近似する多項式を生成できます．あとはπを挟む適当な区間を指定することで，二分法によりπの近似値を計算してみることができます．