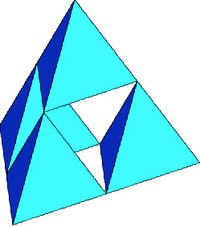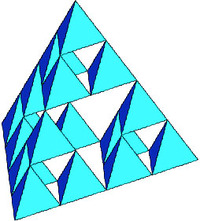解説 -- フラクタルImaginary Cube --

1. シェルピンスキー四面体

まず，正四面体を考えます。正四面体は、3方向から見て正方形に見える、 Imaginary Cube でした。正四面体を、４つの頂点を中心にして１／２に縮小し たものを合わせた立体を考えましょう。この立体を、穴あき四面体４と呼ぶこ とにします。穴あき四面体４は４つの正四面体からなっていて、正四面体の真 ん中に正八面体の穴をあけた形になっています。 穴あき四面体４に対して同じ操作を繰り返しましょう。つまり、元の正四面体 の４つの頂点を中心に穴あき四面体４を１／２に縮小して重ね合わせます。こ うしてできた立体を穴あき四面体１６と呼ぶことにします。同様に、これを繰 り返して、穴あき四面体４n を定義します。
正四面体 穴あき四面体４ 穴あき四面体１６ 穴あき四面体６４

穴あき四面体４n は、４n 個の正四面体からなってお り，その体積は正四面体の 1/2n, その表面積は正四面体と同じで す。シェルピンスキー四面体は，この操作を無限に繰り返して作られる立体で す。より正確には，これらの立体は穴をあけることによりどんどん小さくなっ ていきますが，どの段階でも削られない点集合，すなわち，すべての共通部分 です。



シェルピンスキー四面体に対して、今行ったのと同じ操作、すなわち、４つの 頂点を中心に１／２に縮小して合わせることを考えます。すると、また、自分 自身に戻ることが分かります。このように，シェルピンスキー四面体は，自分 を 1/2 に縮小したもの4つからなっている立体図形です。このような図形を、 自己相似図形といいます。また、どこを見ても全体と同じ構造を持っているよ うな図形をフラクタルといいます。シェルピンスキー四面体は、フラクタル立 体図形の代表例です。

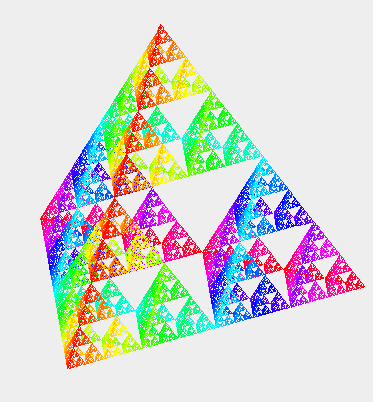
自己相似図形には、相似次元と呼ばれる次元が定義されます。 平面図形の正方形は，1/2 に縮小したものを 4 つ集めたら自分自身に戻るとい う性質を持っています。立体図形の立方体は，1/2 に縮小したものを 8 つ集め たら自分自身に戻るという性質を持っています。このように，n 次元図形は、 1/2 に縮小したものを2n 集めたら元に戻るという性質を持ってい ます。より一般に、1/k に縮小したもの 2n 個集めたら自分自身に 戻ります。この性質でもって、自己相似図形の次元を定義することにしましょ う。つまり、1/k に縮小したもの 2n 個集めたら自分自身に戻ると き、自己相似図形の相似次元が n であると定義するわけです。これは，フラク タル図形一般に定義されるフラクタル次元（ハウスドルフ次元）と一致します。 (ここで，1/k に縮小するとは，1辺の長さを 1/k にするという意味です。)

シェルピンスキー四面体は、1/2 に縮小したもの4つ集めて元に戻るのですから、 相似次元が2次元です。 正四面体は，辺の中点と反対側の辺の中点を結ぶ線の方向から見れば，正方形 に見えるという性質を持っています。すなわち、I-cube です。それは，穴あき 四面体４n についても同様です。このことは数学的帰納法で証明で きます。

そして，その極限であるシェルピンスキー四面体も同様です。この証明には、 極限操作が必要なので、位相的考察が必要になります。上のシェルピンスキー 四面体を，そのような方向から見たら，次の絵のように見えます。

>

つまり、シェルピンスキー四面体は、相似次元が2次元のフラクタルなI-cube です。ある方向から見るというのは、2次元に射影するということです。射影に よって、相似次元は低くなります。よって、I-cube の相似次元は2次元以上で なくてはなりません。2次元の時には、正方形に見えるときに（境界以外では） ちょうど重なりなく、正方形を埋めることになります。 この他にも、相似次元2のフラクタルなI-cube は存在するのでしょうか？

２. 相似次元2のフラクタルなI-cube

相似次元2ということは、自分自身を 1/k に縮小したミニチュア k2 個を集めてもとに戻るということです。ここでは、さらに条件 を狭めて，縮小するときに，図形を回転しないものだけを考えます。すなわち， 自分自身を 1/k に縮小したミニチュア k2 個を平行移動して合せ たら自分自身に戻るものを考えることにします。そういうものの中で、３つの 直交する方向から見て正方形に見えるものということです。そのような立体を X と呼ぶことにしましょう。

X が正方形に見えるということは，それぞれのミニチュアも正方形に見えると いうことです。その小さい正方形 k2 個合わせると，X の像である 正方形に戻るわけですから，そのような k2 個の正方形の配置は， X の像となる正方形を k × k に切ったものしかありえません。それが，３つ の直交する方向で成り立つのです。

X を３つの直交する方向から見て正方形に見えるということは、それらの正方 形から決まる立方体が存在します。3方向の影において、この正方形を k × k に切ったものにミニチュアが１つづつ入っていることから、その立方体を k × k × k に切って，k3 個の立方体の中から k2 個を， どの面から見ても k2 個全てが見えるように選んだものに、それら のミニチュアが入っていることになります。

また、逆に、立方体をk ×k × k に切って，その中から k2 個を， どの面から見ても全てが見えるように選ぶ選び方に対応して、フラクタル I-cube が存在することになります。立方体をこの k2 個の小さな 立方体に置き換えても、3方向から見て正方形に見えますね。つまり、I-cube になります。そして、その操作を、これら k2 個の小さな立方体に 適用しても、そうです。そして、無限にこの操作を繰り返した極限の立体につ いてもそうです。極限の立体というのは、この操作をするとどんどん小さくなっ ていきますが、全てのレベルに存在している、つまり、全てのレベルの立体の 共通部分と考えればいいですね。 そのような選び方は，k = 2 の時には，立体の回転で重なるものを同一視する と、次の一通りしかありません。


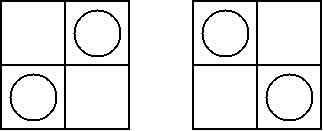
そして、これを繰り返すと、シェルピンスキー四面体ができます。実は、フラ クタルが、初期立体に関係なく縮小写像によってきまることが証明できます。

n=2 の時には，次の図のように，シェルピンスキー四面体を得ることが出来ま す。


> > >

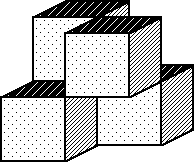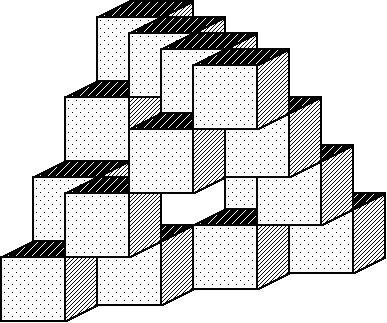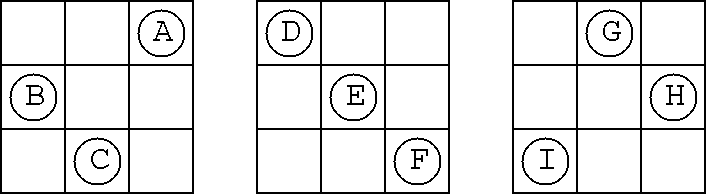
また，k = 3 の時には，次の2通りしかないことが分かります。（他のものを考 えても，立方体を回転させれば，このどちらかと同じになります。）計算によ り，k=4 の時には 36 通り，k=5 の時には 3482 通りあることが分かりました。





k=3 のときのそれぞれの配置でできる立体は，その基本となる立体が 重六角錐と反三角錐台にそれぞれなっています。

また，k=4 の時の 36 通りの中の，このアプレットで表示して 32番目のものは， k=4 の立体の中で，唯一連結なものです。これは，基本となる立体が立方八面 体を変形した形となっています。

それぞれの立体がどのようなものになるか，アプレットで見て確かめてください。