(フラクタル)反三角錐台 (T)
--- 三角柱と三角錐と正八面体に関係した Imaginary Cube ---

三角柱の片方の底面の各辺の中点をとり，
もう片方の底面の頂 点を結び，その外側を切り落とします。
そうして出来る8面体のことを，反三角錐台と呼ぶことにします。
    

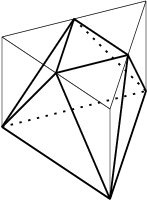
ここで興味があるのは，底辺の辺の長さに対して，高さが √３／２√２ である反三角錐台です。 そのような反三角錐台を， T と呼ぶことにします。
この反三角錐台は，見る方向を選べば，正方形 に見えます。

          上の写真は，一つの方向とその逆の方向から見たものです。
正方形に見える方向は３つ（逆方向を区別したら６つ）あり，それらは直交しています。
すなわち， T は I-cube です。
このことは，立方体の箱に入れて考えると分かりやすいです。

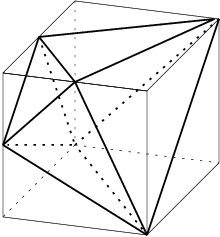
この反三角錐台は，もう一つ面白い性質を持っています。
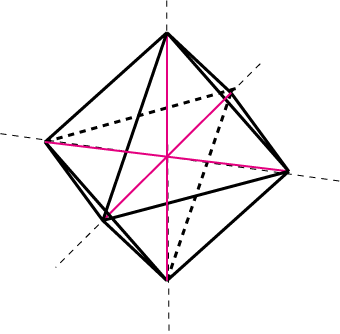
３次元の座標軸の上で， 正の方向と負の方向に同じ距離の点を結べば，正八面体ができます。
それに対し， 正の方向１に対し負の方向２の距離の点を結べば，T ができます。

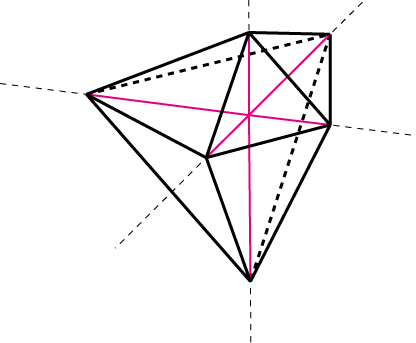正八面体	反三角錐台

実際，T を頂点の方向から見れば，
二つの対角線が直交しており，中 心点が１：２に内分していることが分かります。

---

さて，T に対して，６個の頂点と大きい底面の３辺の中点の９点を
中心として，１／３の縮小を行ってできた，
小さな T ９個 を合わせた立体を考えます。

それでも，先ほど正方形になった6つの方向から見ると，正方形のままです。

さらに，先ほどと同じ縮小を行い，もっと小さい T ８１個にしても，同 じです。

この操作を，無限に繰り返した極限の図形を考えても同じです。
３方向か らみて正方形に見える相似次元２の自己相似図形（フラクタルな I-cube）にな ります。

下のアプレットで，この立体を， x 軸，y 軸，z 軸の回りで回転させることが できます。
いろんな方向から見てください。

Java2 に対応したブラウザで見てください。

上のラジオボタンで Hexagonal を選ぶと， もう一つの図形，重六角錐によるフラクタルが現れます。

なぜ正方形に見えるのか？
それについては， フラクタル Imaginary Cube の解説 および， 数学セミナー 2006年10月号の説明をごらんください。

この立体を回転する途中に見える形をいくつか載せておきます。
一つの立体を回転させる途中に見える図形の多彩さを味わってください。