解説

このパズルのピース間に隙間のない解は、箱の回転を除いて一通りしかありません。
それは、このような三回対称性をもった奇麗な形をしています。
ピース間に隙間のある入れ方はたくさんあります。
今見つかっているのは,隙間のない解と同様に,真ん中に T を入れるものだけです。
それ以外の解があるかどうかは分かっていません。
ピース間に隙間のある入れ方はたくさんあります。
今見つかっているのは,隙間のない解と同様に,真ん中に T を入れるものだけです。
それ以外の解があるかどうかは分かっていません。
ピースの間に隙間のある解で,箱の真ん中に T を入れるものは,。
512 通りあります(箱の横回転で重なるものは同一視し,鏡像を同一視しない場合)。
鏡像となる入れ方を同一視すると,276 通りあります。
さらに,箱の3次元的な回転で同じものも同一視すると,52 個あります。
鏡像となる入れ方を同一視すると,276 通りあります。
さらに,箱の3次元的な回転で同じものも同一視すると,52 個あります。
- テセレーションデザイン協会の荒木義明さんが, 136 通り(276通りの中で真ん中のTを固定したもの)の図を作ってくれました。
- この計算を行った Python プログラム および, その google colab へのリンク です。
- 512 が2ベキの数であることに意味はないと思われますが,神秘性を感じます。
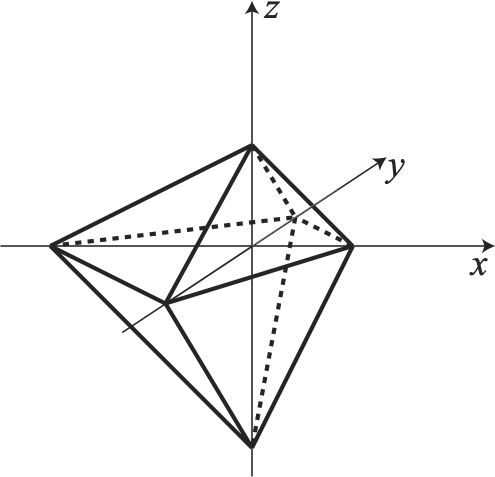
このパズルは、全ての頂点が3次元座標軸上に来る様に T を
配置できることと深く関わっています。詳しくは,下のスライドをご覧ください。

また,このパズルは、H と T がこの 3 次元空間をうめつくすこととも
関係しています。詳しくは,下のスライドをご覧ください。