H‑Fractal

The solid H is shown below.

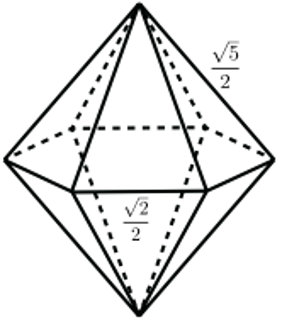
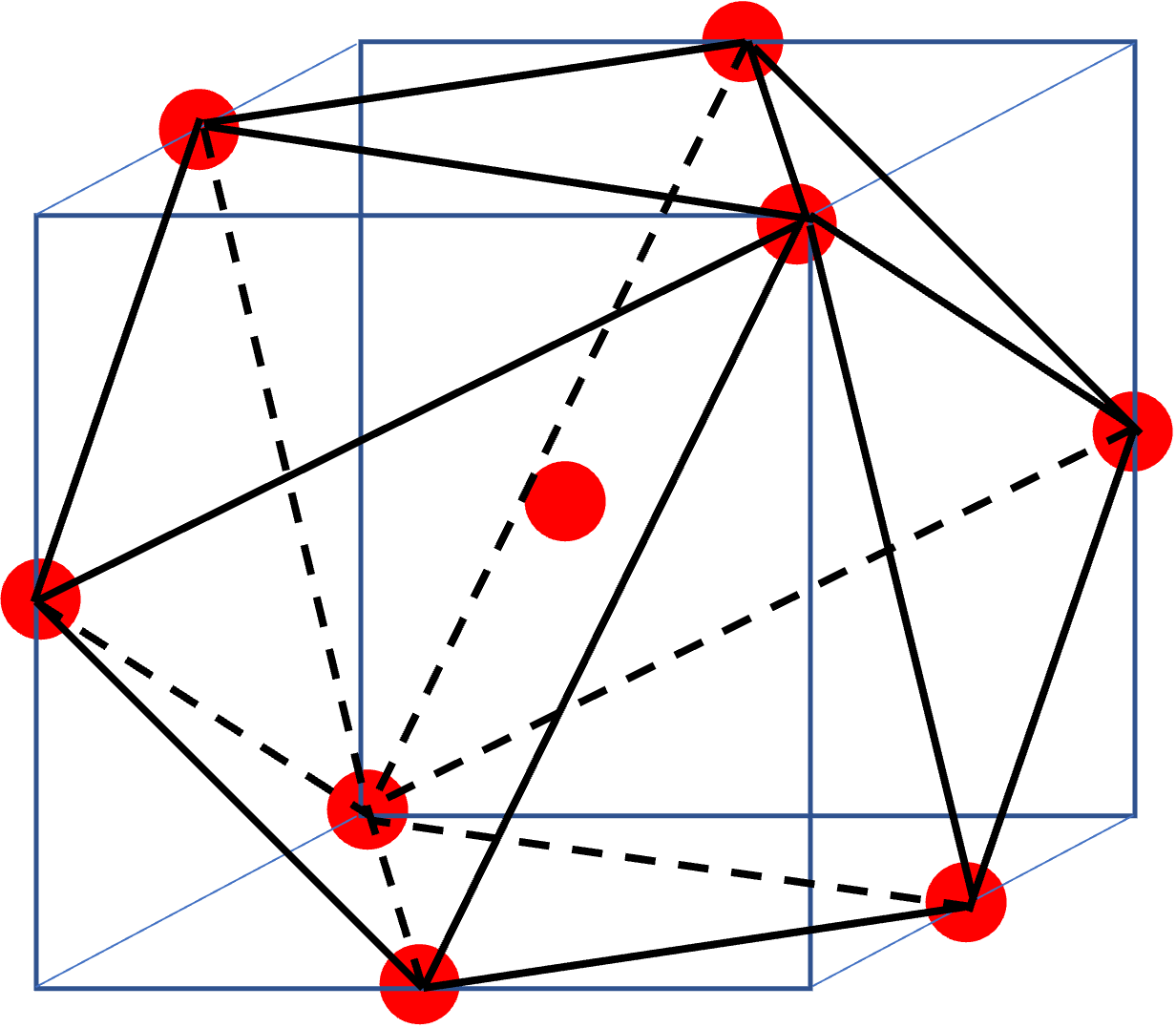
Like the Sierpinski Tetrahedron, the H‑Fractal is obtained by repeatedly assembling scaled‑down copies of H. Mark the nine red points in the figure above (the eight vertices of H plus its center). Shrink H by 1/3 about each of these nine points and combine the copies to form H₁. Apply the same procedure to H₁ to obtain H₂, and so on, producing the sequence H, H₁, H₂, …

The limiting solid (more precisely, the common intersection of all H_n) is the H‑Fractal. If you shrink the H‑Fractal itself by 1/3 about the same nine points and re‑assemble the copies, you obtain the original again. Thus the H‑Fractal is a self‑similar object made from nine copies scaled by 1/3.

H‑Fractal as an Imaginary Cube

The photos below show 3‑D‑printed models of H, H₁, H₂, H₃, … packed inside cubic boxes. Every model is an Imaginary Cube.

The limiting H‑Fractal itself is also an Imaginary Cube. Remarkably, the H‑Fractal appears as a square not only from the three orthogonal directions of a cube but from six directions. In fact, a single H‑piece fits inside a cube in two distinct orientations (rotated by 60 °), so H is a “double Imaginary Cube.” The H‑Fractal inherits this property and is likewise a double Imaginary Cube.

Shadows of the H‑Fractal

The shadows (projections) of the H‑Fractal are self‑similar as well. Rotating a physical approximation under a light source produces a continuum of changing silhouettes, as shown below. For the ideal fractal, most shadows have area 0, but some—including the square and the examples here—have positive area.

The second silhouette has the outline shown below. This outline is self‑similar: it can be reconstructed from nine copies scaled by 1/3. Can you see how?

In the colored version each color is one of the nine scaled copies; taken together they recreate the original shape.

Which light directions produce shadows with positive area? This question is discussed in the chapter Fractal Shadows.