Sierpinski Tetrahedron
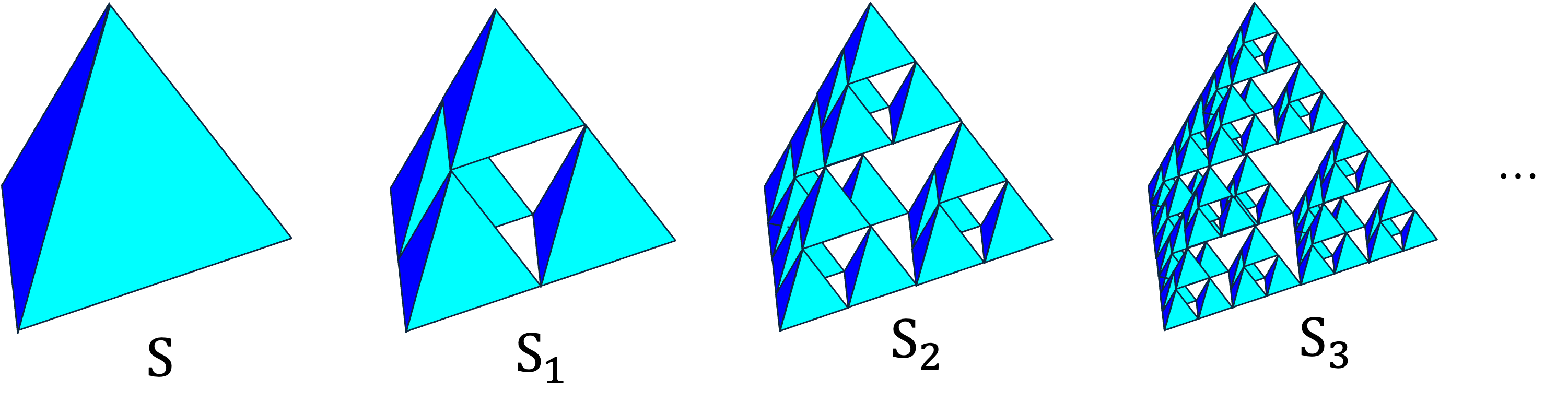
Begin with a regular tetrahedron S. Shrink it to half size about each of its four vertices and assemble the four copies: the result is a “holed” tetrahedron S1. Repeat the same procedure on S1 to obtain S2, which consists of 16 smaller tetrahedra. Applying the process once more yields S3 with 64 tetrahedra, and so on. This produces an infinite sequence S, S1, S2, S3, … of ever‑smaller solids. The Sierpinski Tetrahedron is the limiting solid (more precisely, the common intersection of all Sn).
If you shrink the Sierpinski Tetrahedron itself by 1/2 about each vertex and re‑assemble the four copies, you obtain the very same object again. A shape that can be reconstructed from scaled‑down copies of itself is called self‑similar. More generally, whenever every magnified part exhibits the same structure as the whole, we call the object a fractal.
Sierpinski Tetrahedron as an Imaginary Cube
The photos below show 3‑D‑printed models of S, S1, S2, S3, … packed inside cubic boxes. Each model is an Imaginary Cube; try to see why while examining the pictures. (A proof can be given by mathematical induction.)







The limiting Sierpinski Tetrahedron itself is also an Imaginary Cube, although proving this requires some topological arguments usually taught at the university level.
Shadows of the Sierpinski Tetrahedron
The shadow (strictly speaking, the projection) of the Sierpinski Tetrahedron is likewise self‑similar. Rotating a physical approximation of the tetrahedron under a light source produces a continuum of changing silhouettes. Because it is an Imaginary Cube, one of those silhouettes is of course a square, but many other beautiful shapes appear.

For the exact fractal, almost all shadows have area 0. Nevertheless, besides the square there are projections with positive area, such as the one below.

That shadow has the outline shown here—a self‑similar figure that can be reconstructed from four copies scaled by 1/2. Can you see how?

In the colored version below, each color is one of the four half‑size copies; together they recreate the original shape.
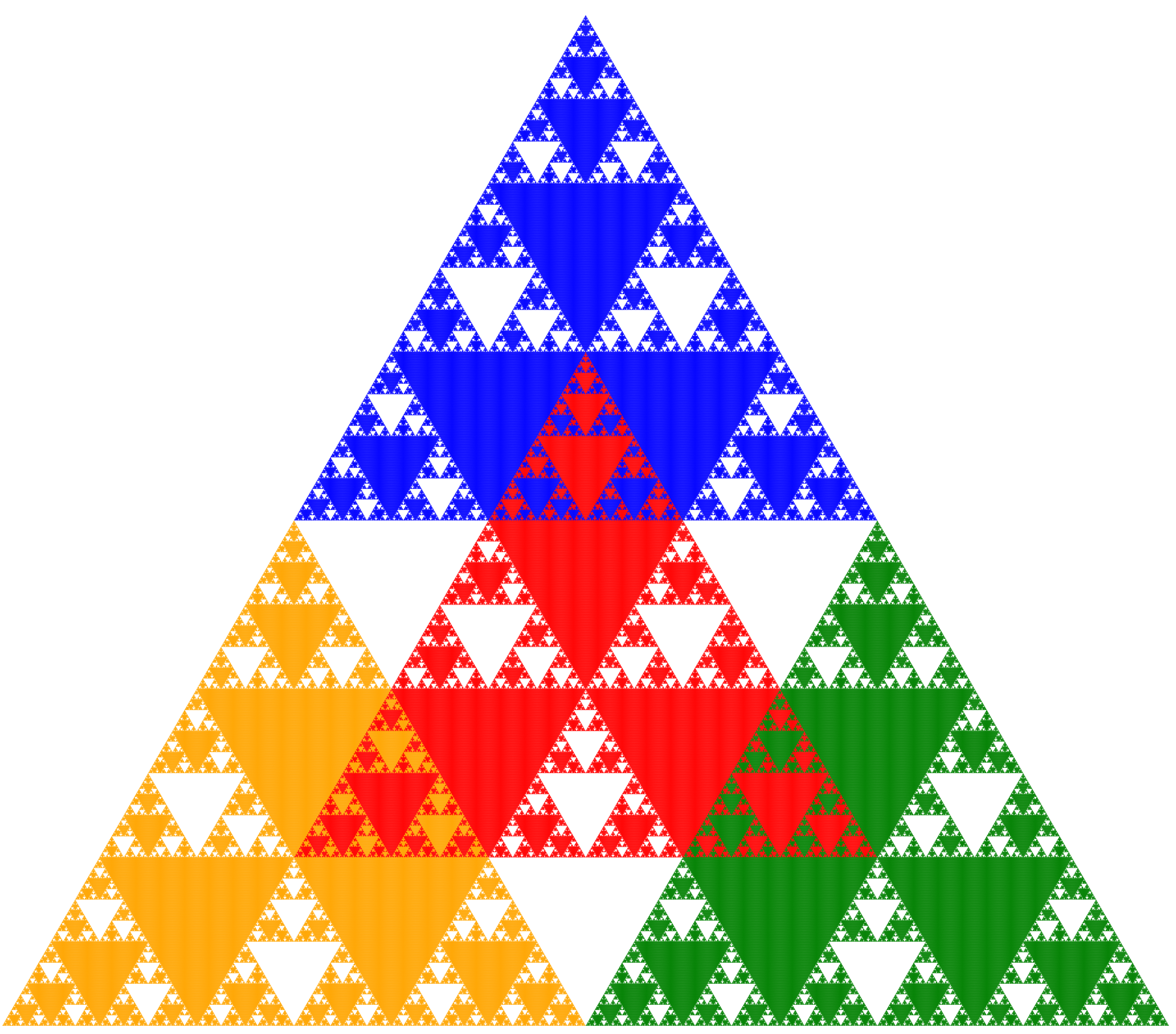
The next silhouettes also arise as shadows of the Sierpinski Tetrahedron and are therefore self‑similar. Can you identify the self‑similarity?



The first silhouette is built from four half‑size copies arranged as shown:

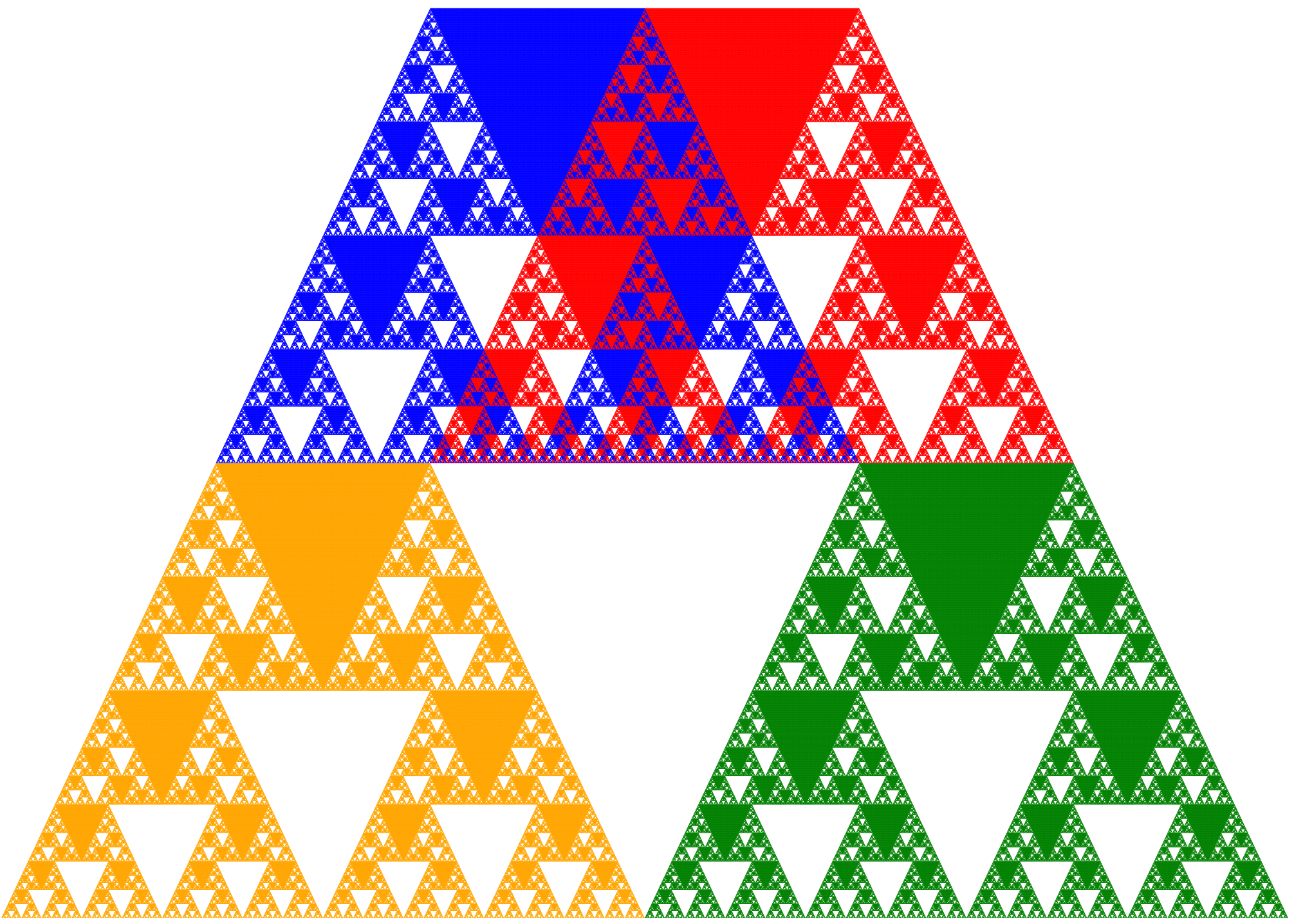
The second silhouette is the classic Sierpinski Triangle. It can be formed from three half‑size copies, but here two of them overlap perfectly, so in effect four half‑size shadows are involved. The third silhouette also consists of four identical shapes that overlap partially. These two shadows have positive area for the physical approximation, but would have area 0 for the ideal fractal.
Thus, some shadows of the Sierpinski Tetrahedron have positive area while others do not. Which viewing directions produce shadows with area? This question is addressed in the chapter Fractal Shadows.