Light Directions That Produce Shadows with Positive Area

For each of the three fractal Imaginary Cubes—the Sierpinski Tetrahedron, the H‑Fractal, and the T‑Fractal—some directions of light yield shadows with positive area (including squares), while others give shadows of area 0. What determines whether a shadow has area?

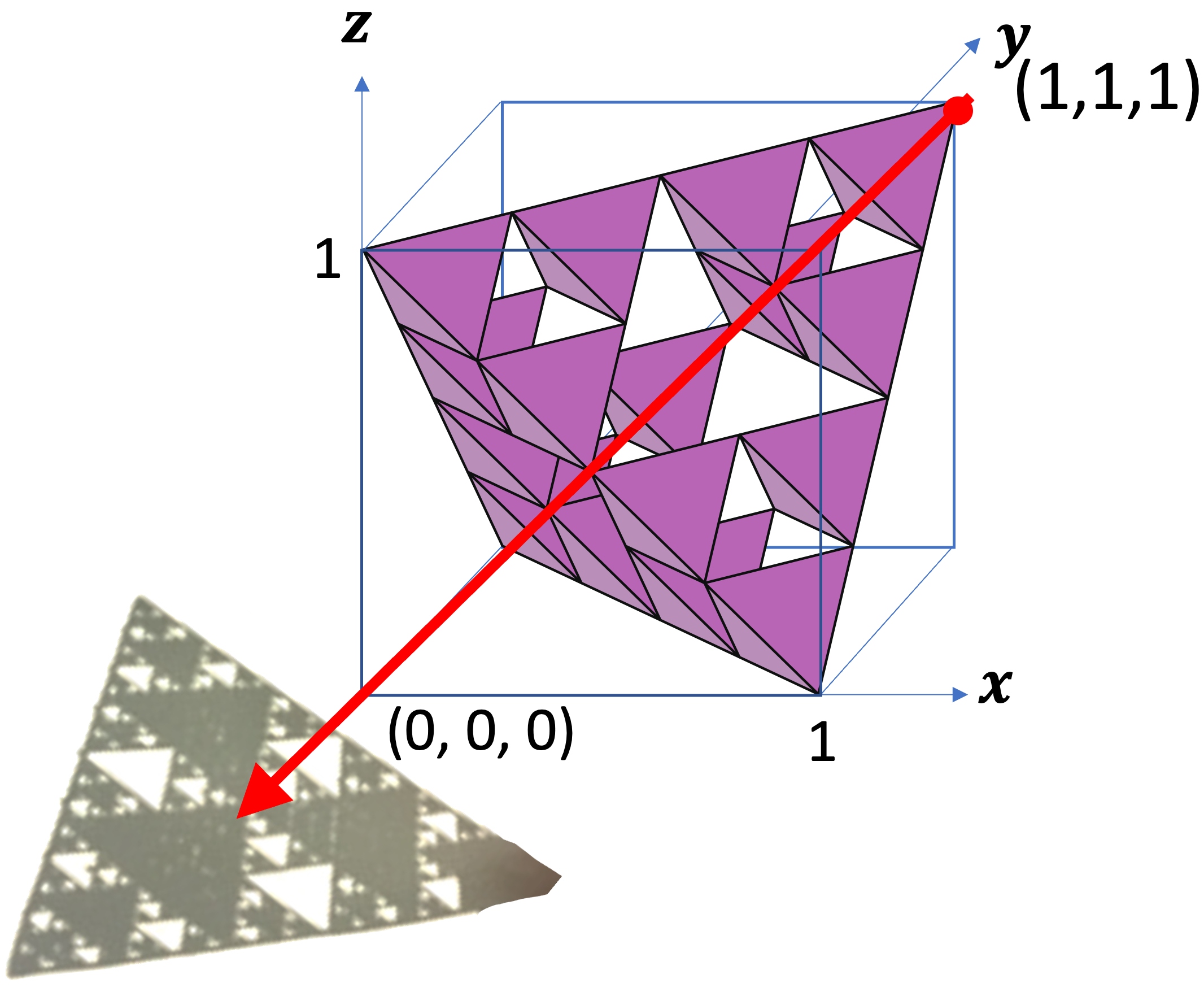
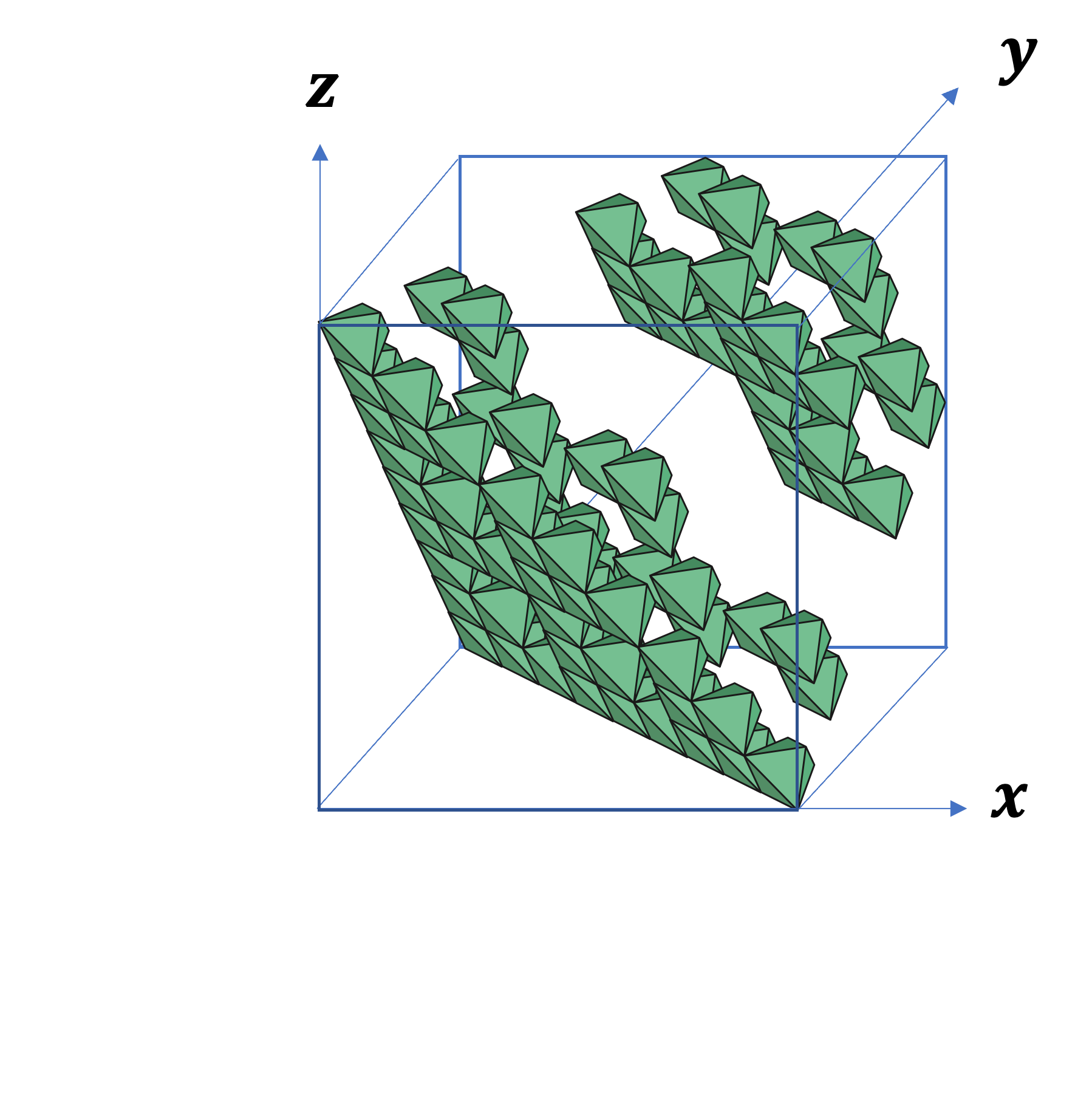
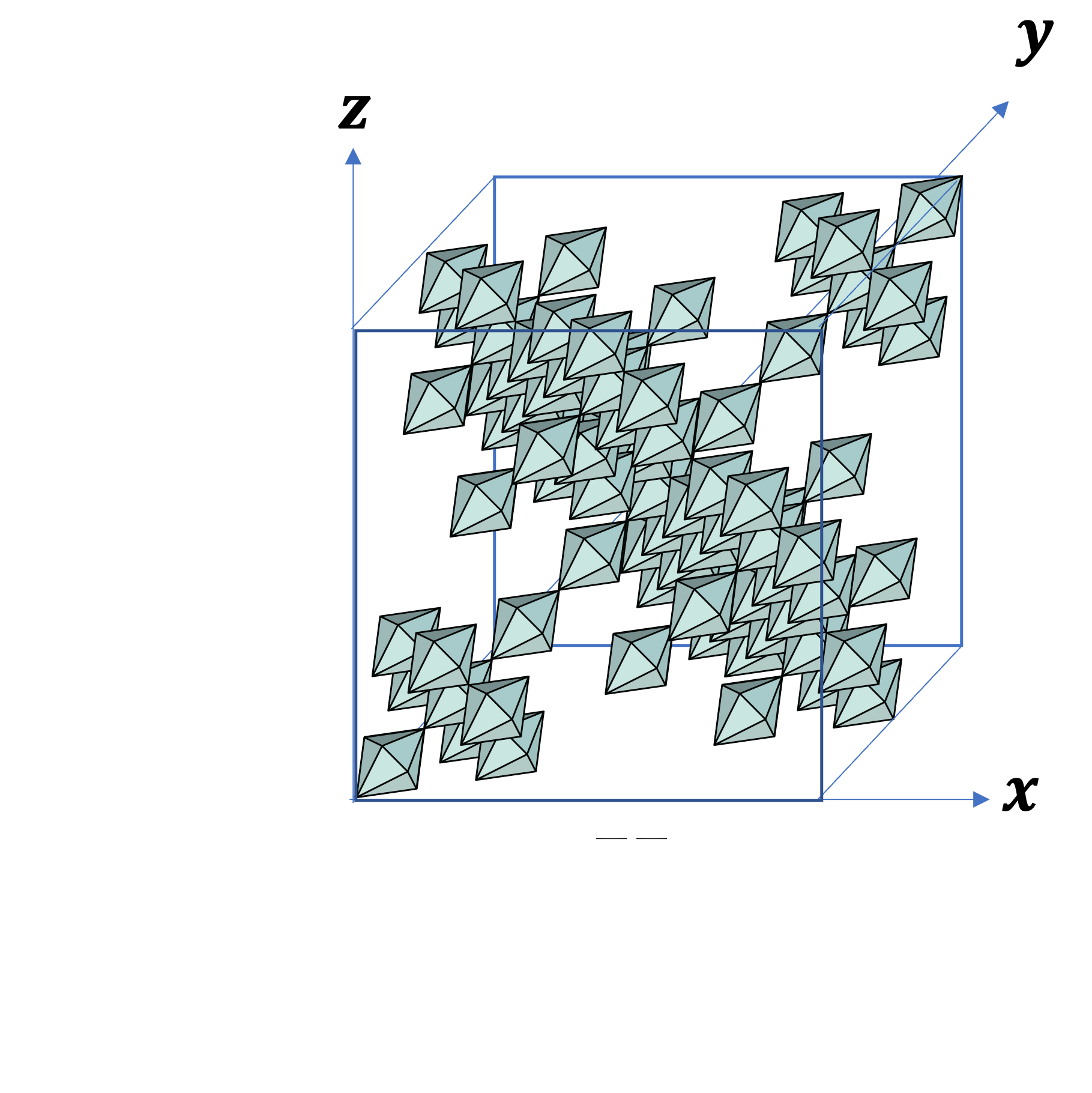
Place each fractal inside a unit cube as shown above. Label the front‑left‑bottom corner of the cube as the origin, and let the three edges be the x, y, z axes. Suppose light shines from the point with coordinates (a, b, c) toward the origin. Then the following holds:

• If any of the ratios a : b, b : c, or c : a is irrational, the shadow has area 0.
• Otherwise—that is, if a, b, c are rational multiples of one another—you may scale them so that all three are integers. Dividing by their greatest common divisor lets you assume that a, b, c are coprime. In that case:
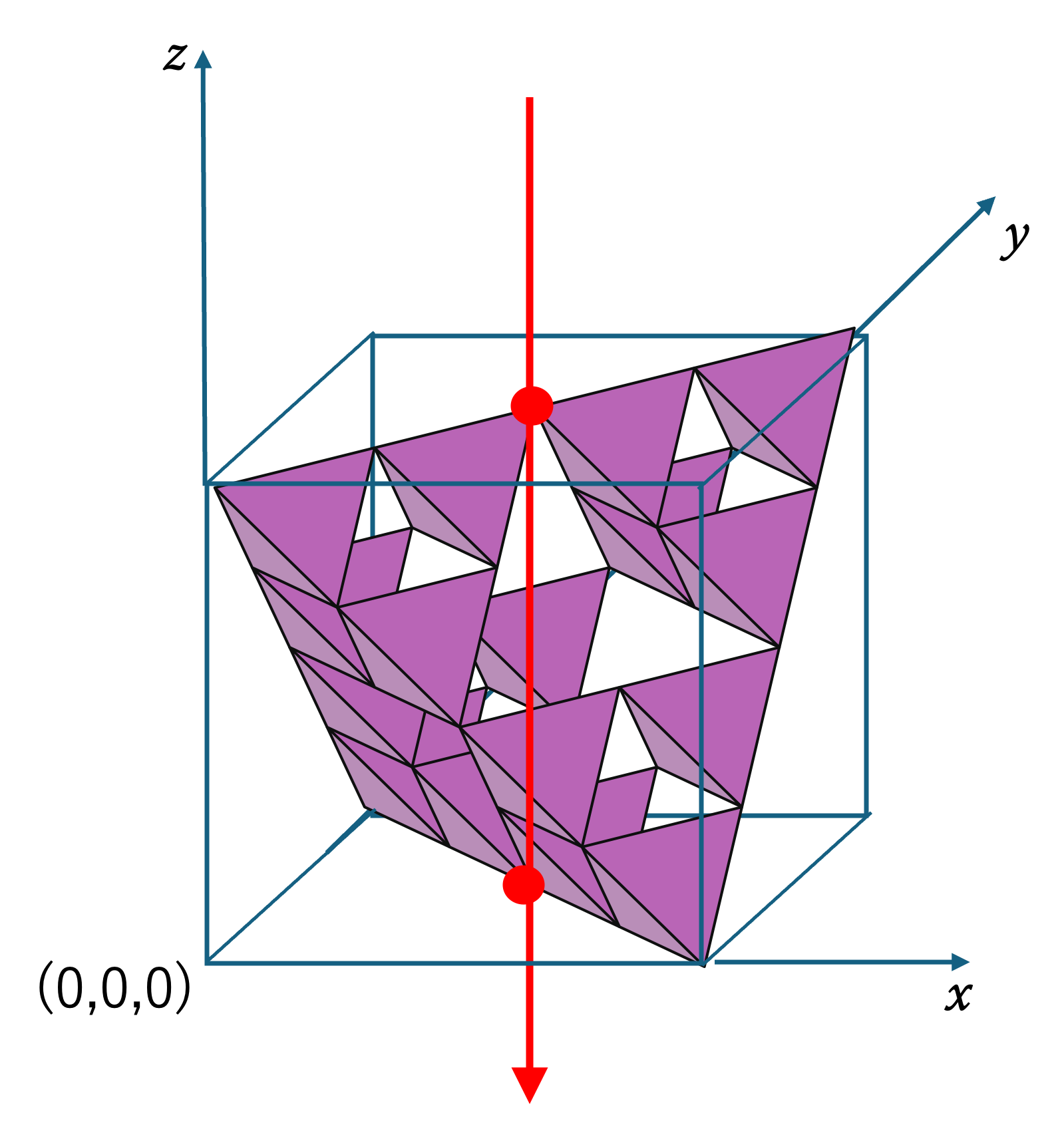
  • Sierpinski Tetrahedron: the shadow has positive area iff a + b + c is odd; otherwise its area is 0.
  • T‑Fractal: the shadow has positive area iff a + b + c is not divisible by 3; if it is a multiple of 3, the area is 0.
  • H‑Fractal: the shadow has positive area if either (i) a + b + c is not divisible by 3, or (ii) the remainders of a, b, −(a + b + c)/3 modulo 3 are all 1 or all 2. A short calculation shows that rotating a direction that satisfies (i) by 60 ° about the line x = y = z yields a direction satisfying (ii).

The abundance of square‑shadow directions for the H‑Fractal, compared with the T‑Fractal, is related to the fact that the H‑Fractal is a double Imaginary Cube.

These results have been proved for a broader family called Layered Fractal Imaginary Cubes. For details see this paper.

Examples

Let’s confirm the rules with concrete examples. Try to predict the shadow from each light direction and picture.

• (0, 0, 1)

  

  These three squares are projections from the axis directions (1, 0, 0), (0, 1, 0), (0, 0, 1). Since 1 + 0 + 0 = 1 is odd and not a multiple of 3, each shadow has positive area. For H the same square also appears from (−1, 2, 2), (2, −1, 2), (2, 2, −1).

• (1, 1, 1)

  

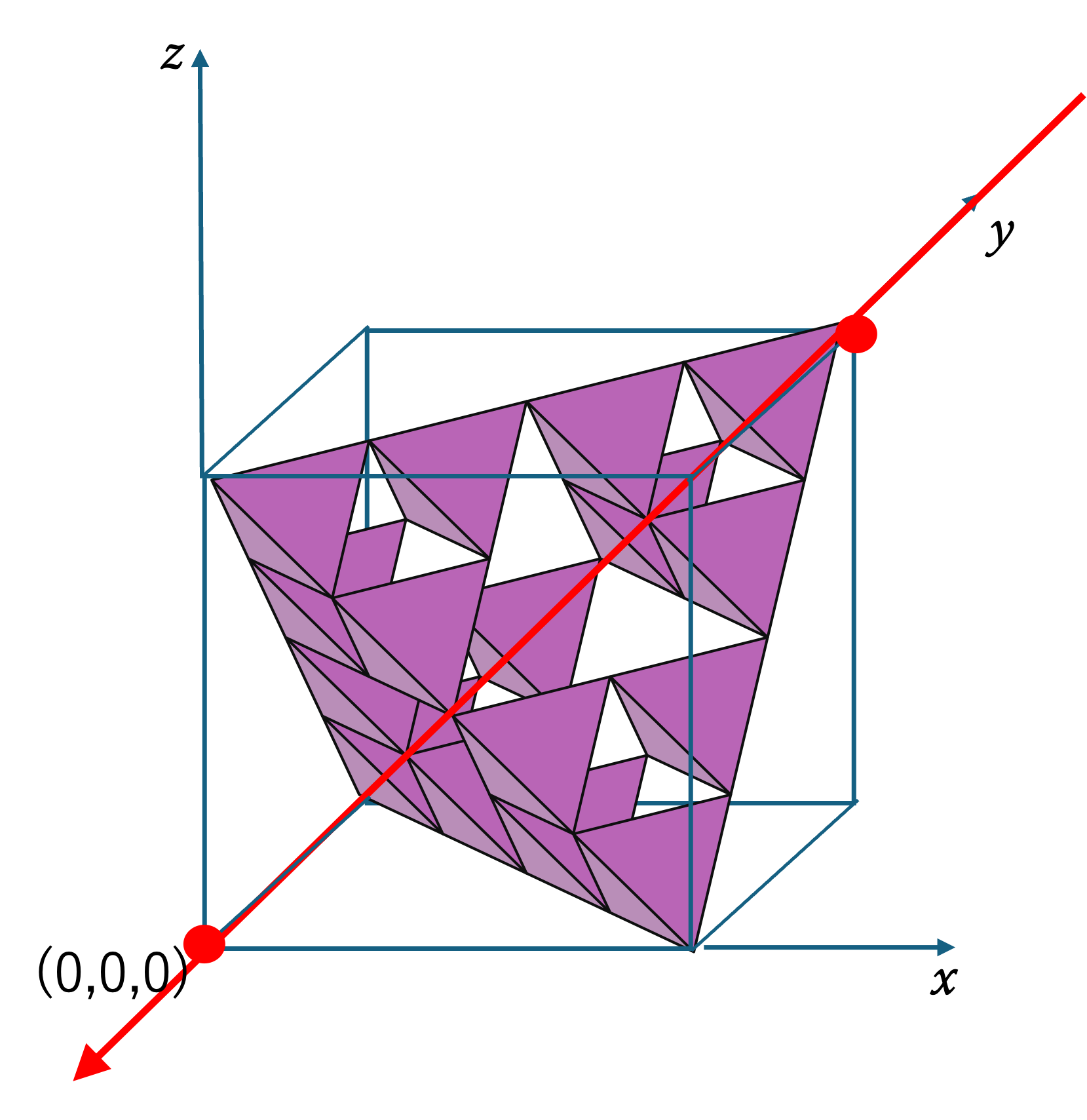
  Here the light comes from (1, 1, 1). Because 1 + 1 + 1 = 3 is odd but divisible by 3, the S‑shadow has area, while the H‑ and T‑shadows have area 0.

• (1, 1, 0)

  

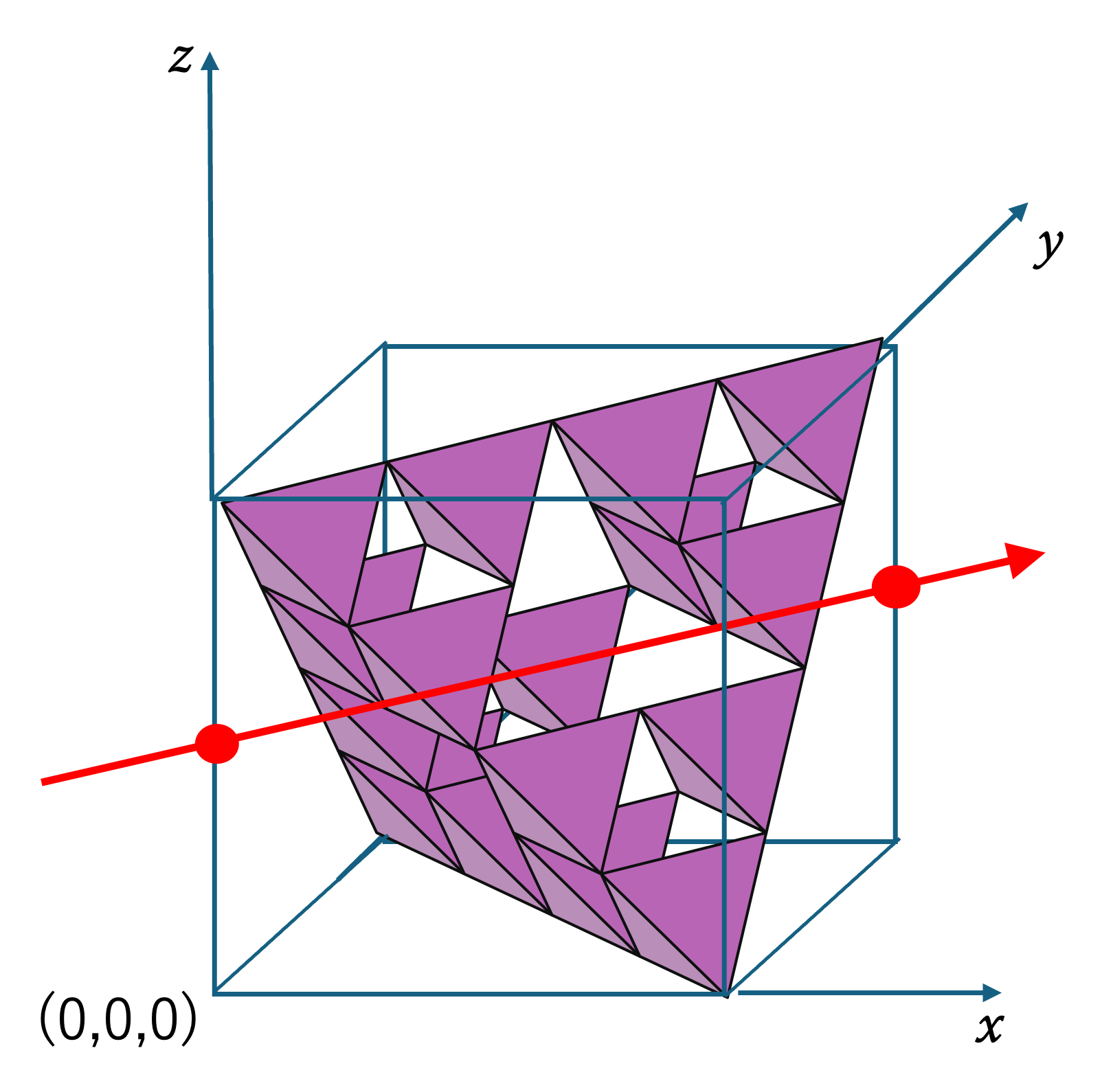
  This projection comes from (1, 1, 0) and also from (0, 1, 1) or (1, 0, 1). Since 1 + 1 + 0 = 2 is even but not divisible by 3, the S‑shadow has area 0, while the H‑ and T‑shadows have positive area. The same H‑shadow appears from (1, 0, 4), (0, 4, 1), and (4, 1, 0).

• (1, 1, −1)

  

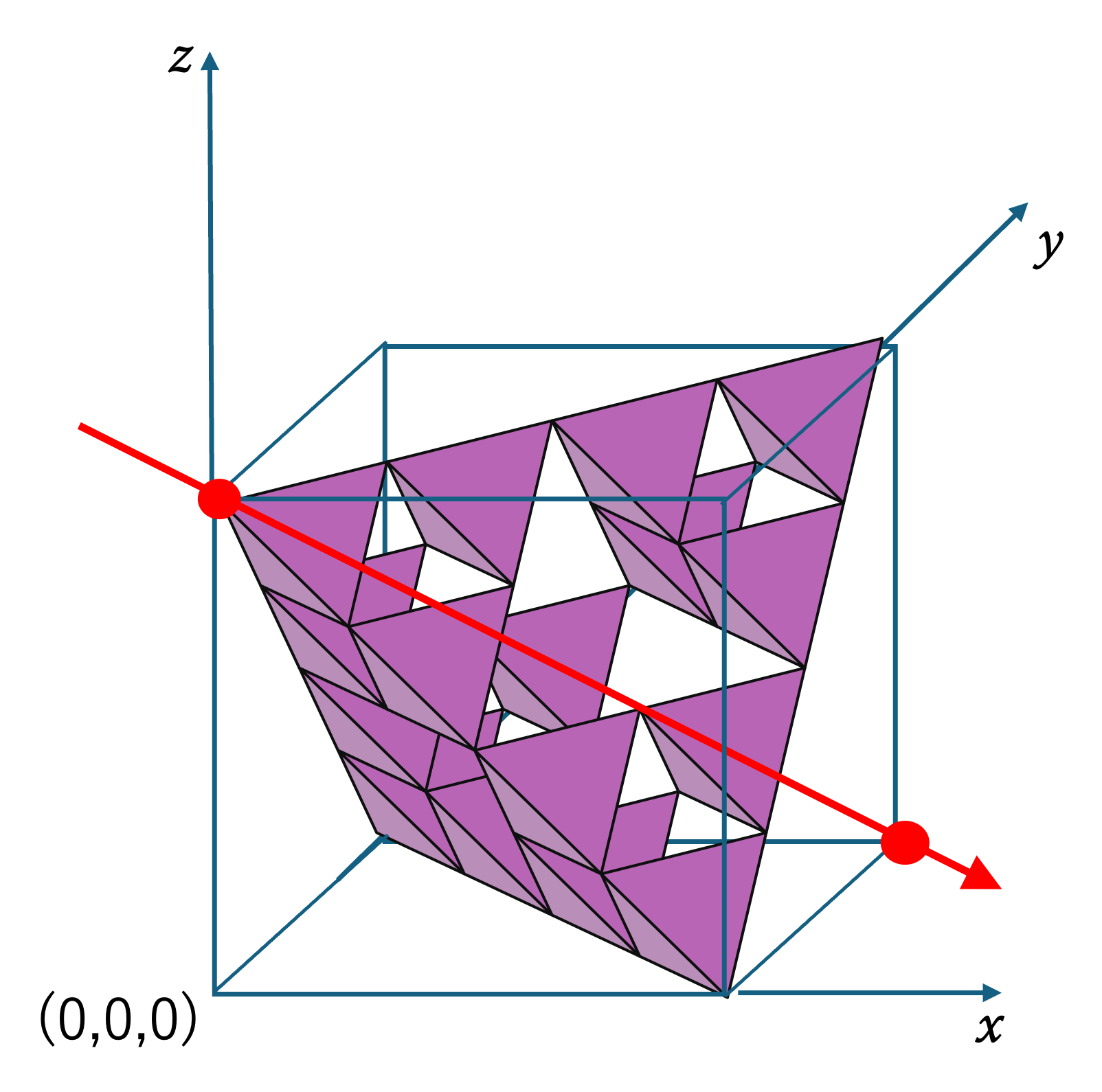
  Light from (1, 1, −1) (or (−1, 1, 1), (1, −1, 1)). Because 1 + 1 + (−1) = 1 is neither even nor a multiple of 3, every shadow has positive area. The same H‑shadow also appears from (1, 1, −5) and its rotations.

• (1, 1, −2)

  

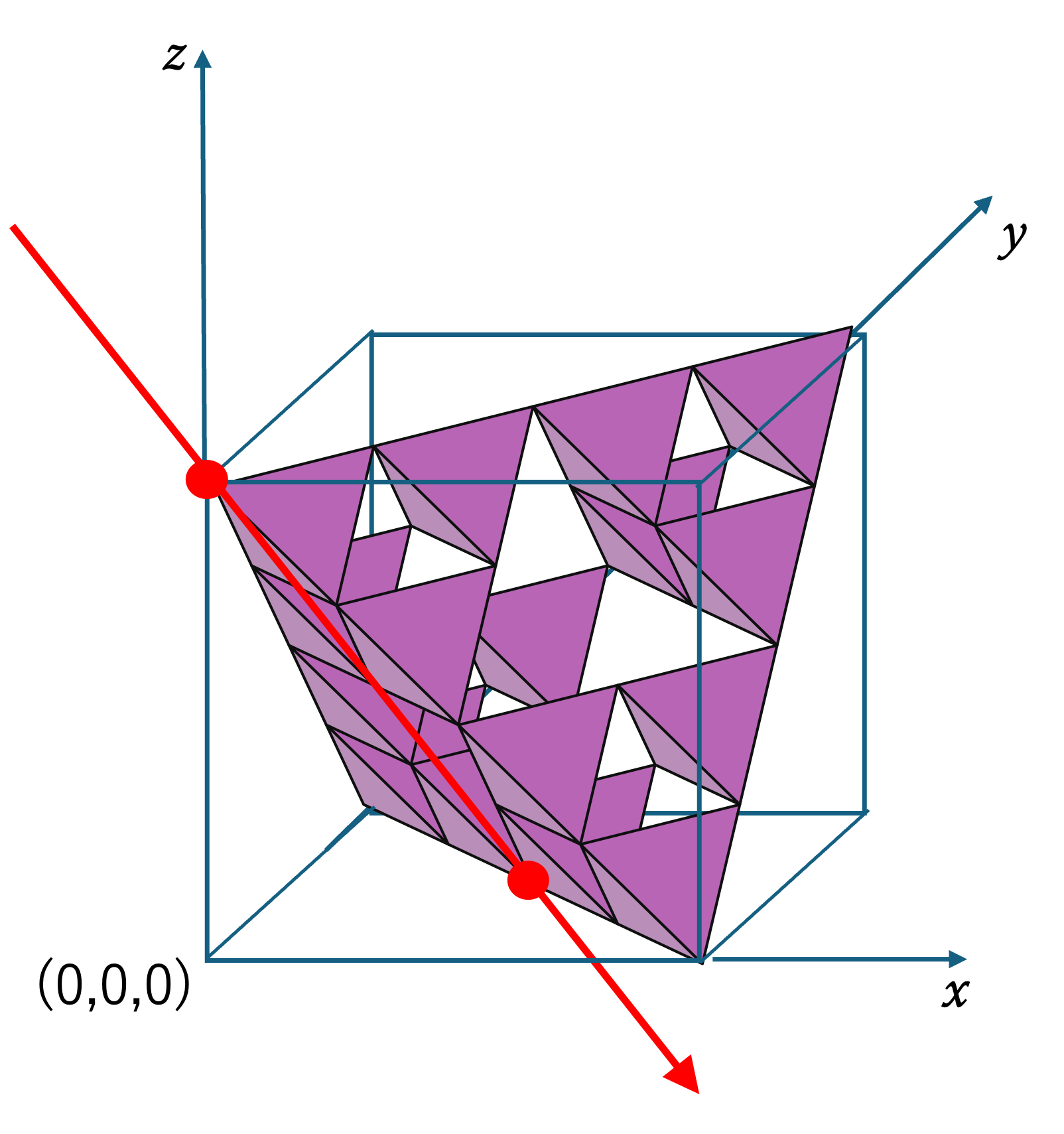
  Finally, (1, 1, −2) (or (−2, 1, 1), (1, −2, 1)). Because 1 + 1 + (−2) = 0 is both even and divisible by 3, all three shadows have area 0.