シェルピンスキー四面体

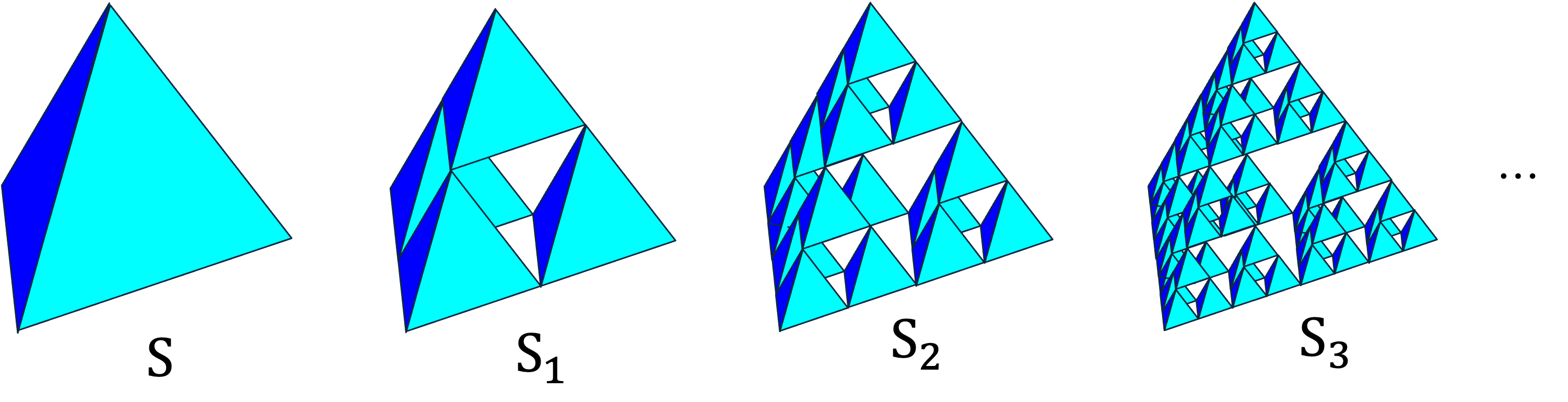
正四面体 S の 4 個の頂点を中心にして S を 1/2 に縮小したものを合わせると，穴あきの正四面体 S₁ ができます。次に，4 個の頂点を中心にして S₁ を 1/2 に縮小したものを合わせてると，16 個の正四面体からなる立体S₂ ができます。S₂ に対してまた同じことを行い，64 個の正四面体からなる立体S₂ を作ります。これを繰り返すと，立体がどんどん小さくなっていく列 S, S₁, S₂, S₃, .. ができます。 これを無限に続けていってできる立体（より正確には， S, S₁, S₂, S₃, .. 全ての共通部分）をシェルピンスキー四面体といいます。

シェルピンスキー四面体に対して 4 個の頂点を中心にして 1/2 に縮小してできる4個の立体を合わせた立体をつくっても，元のシェルピンスキー四面体に戻ります。このように，自分自身を縮小したものをいくつか合わせると元の図形に戻る様な図形は，自己相似図形と呼ばれています。また，より一般に， どの部分を拡大しても，全体と同じ様な構造が存在している時，そのような構造をフラクタルといいます。

シェルピンスキー四面体はイマジナリーキューブ

下の写真は，立方体の箱に入れた S, S₁, S₂, S₃,... を3Dプリントで作成したものです。 これらの立体は，全てイマジナリーキューブです。写真を見ながら考えてください。(このことは，数学的帰納法で証明できます。)

そして，その極限のシェルピンスキー四面体もイマジナリーキューブです。(そのことを証明するには，大学で習うような位相的な考察が必要になります。)

シェルピンスキー四面体の影

シェルピンスキー四面体の影も自己相似図形です。（シェルピンスキー四面体は物理的に作ることができないので，その影を考えること自体がナンセンスで，「射影」という数学用語を使うべきです。しかし，ここでは，影という言葉で通します。）シェルピンスキー四面体の近似模型を，光のもとで回転させると，影が連続に変化していきます。シェルピンスキー四面体はイマジナリーキューブなので，その中にはもちろん，正方形もあります。

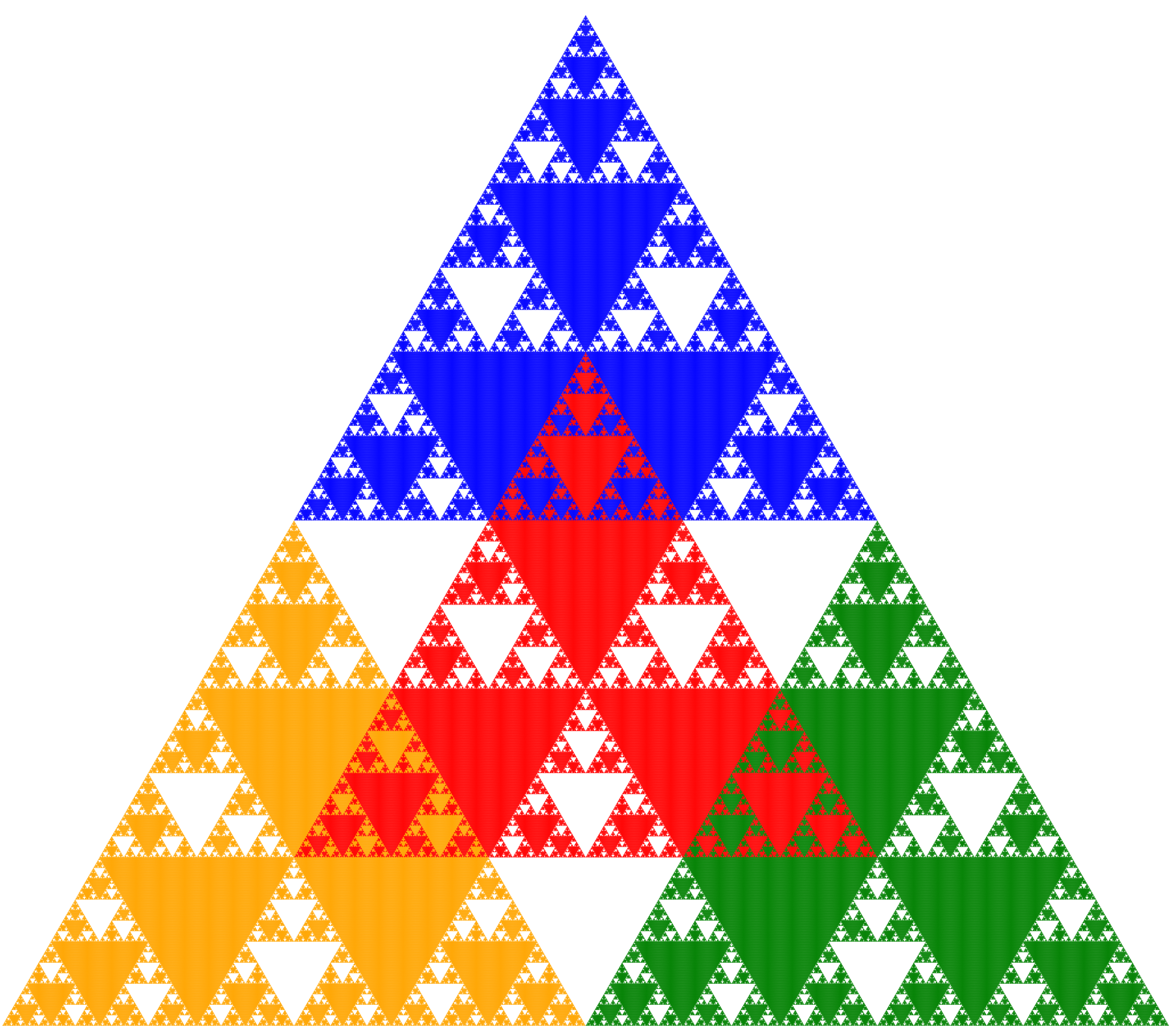
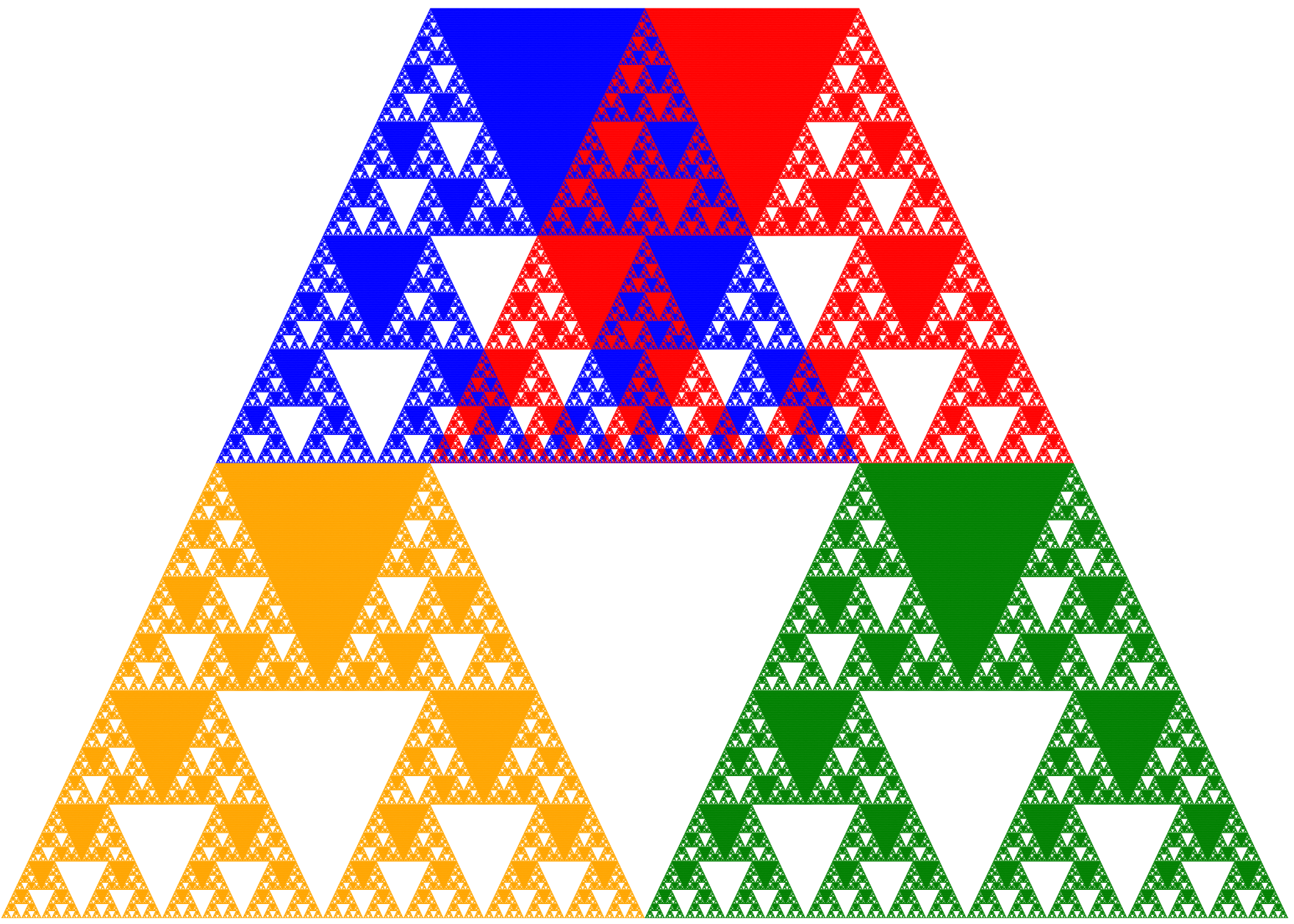
このように，シェルピンスキー四面体の影は，面積をもつものと，持たないものがあることがわかります。どういう方向から光をあてると，面積をもつ影ができるのでしょうか？それについては，「フラクタルの影」の章で説明します。