このパズルの説明
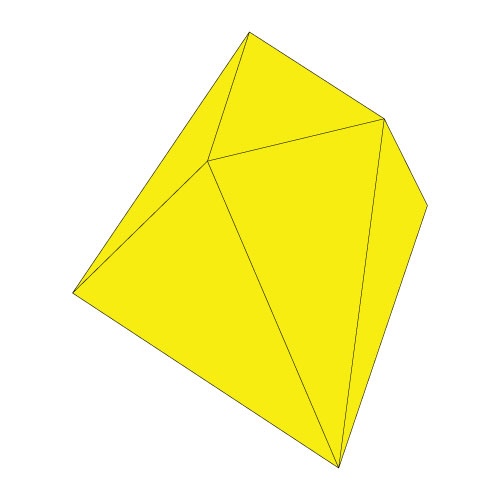
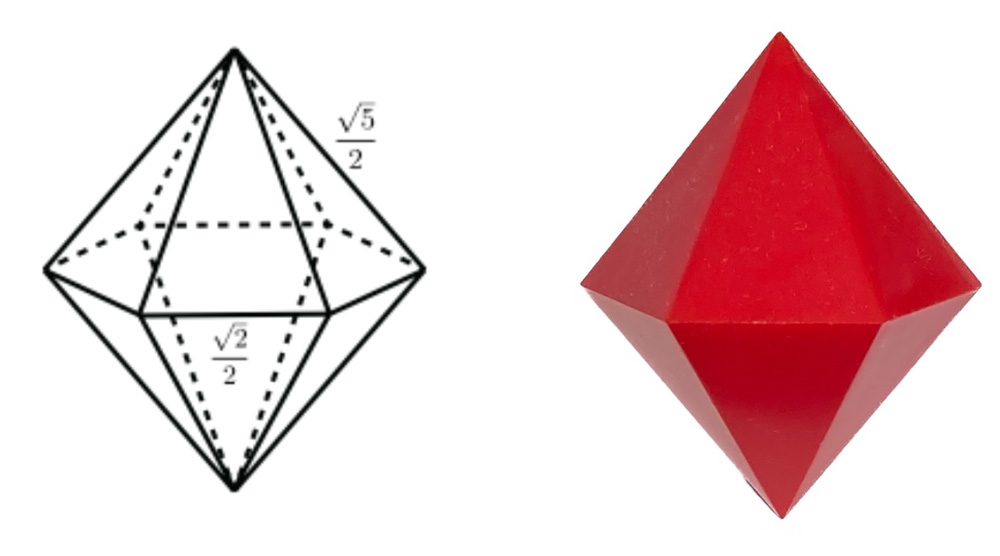
重六角錐イマジナリーキューブ(Hexagonal Bipyramid Imaginary Cube、省略して H と呼びます)は、図のように 2つの正六角錐を底面で貼り合わせた形です。
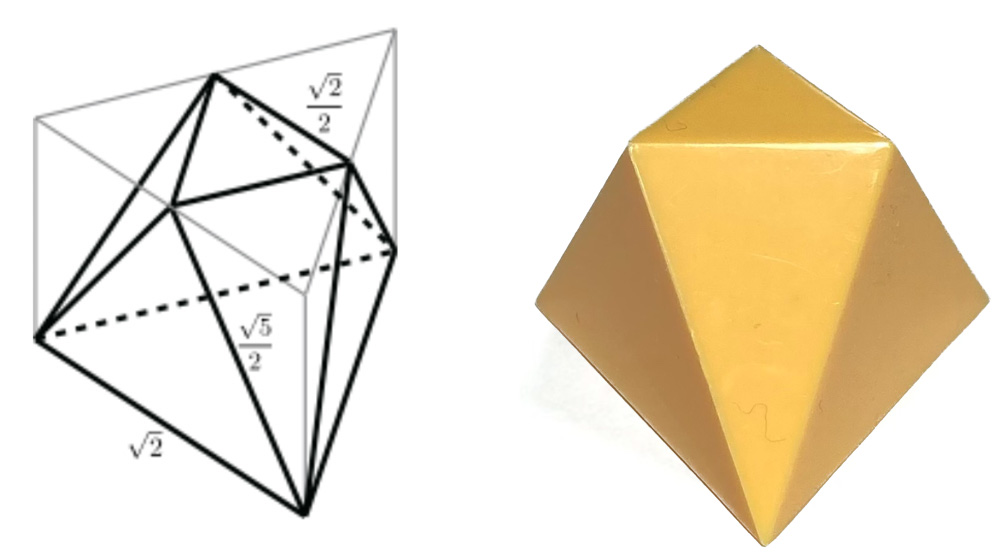
反三角錐台イマジナリーキューブ(Triangular Antiprismoid Imaginary Cube、省略して T と呼びます)は、 図のように正三角柱の片方の面の頂点の周りを切り落とした形です。
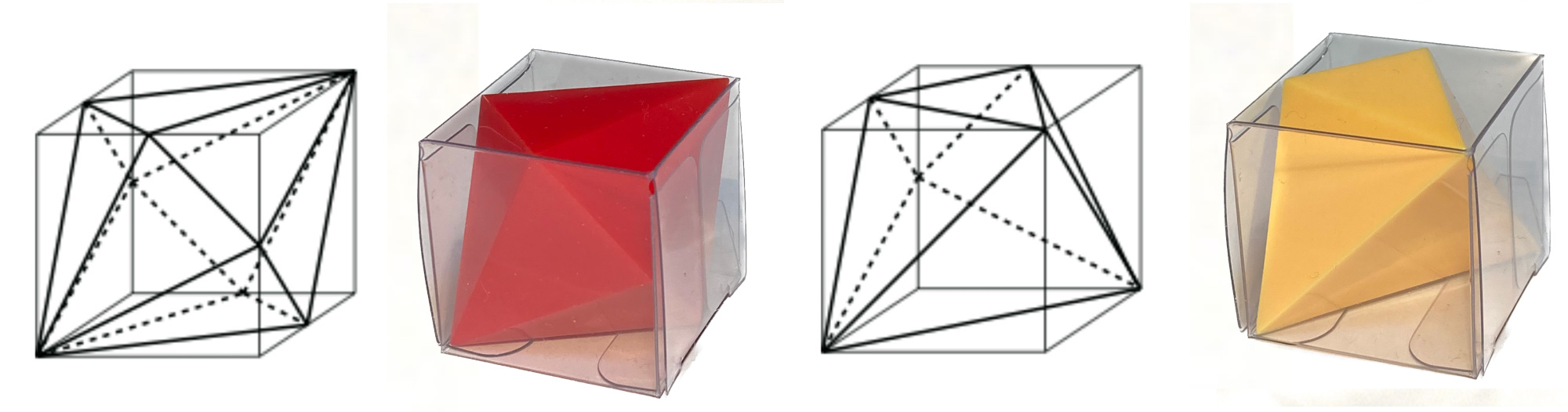
H と T は、辺の長さ1の箱にきれいにおさまり、それぞれ箱の各面から正方形に見えます。このような立体をイマジナリーキューブと呼ぶのでした。
さて、「イマジナリーキューブパズル 3H=6T 」はこの2倍の大きさの箱に H 3個と T 6個を入れるパズルです。箱が2倍の大きさなのだから8個入るのは自明ですが、ここには 9個あります。9個どうやって入れるのでしょう?

このパズルは,解くこと自体も面白いですが,できあがった形から数学の面白さを体感できます。パズルが手元になくても,「ヒントと解法」そして「解説」と読み進めるだけで,十分パズルを楽しめます。そうして仕組みが分かった後に手にしても,楽しめるようなパズルです。
イマジナリーキューブパズル 3H=6T
これは、全部で9個ある2種類の立体を立方体の箱に収める数学パズルです。8個までなら簡単に入りますが、9個目をどうやって収めるのでしょうか?
一見、不可能にも思えるこの課題。しかし、このパズルにはとても美しい解が存在します。最後のピースがケースに収まる瞬間、その完成した形の美しさに驚かされることでしょう。
しかし、そこで終わりではありません。眺めているうちに、「なぜこんなにぴったり収まるのだろう?」「本当に箱の中にきちんと収まっているのだろうか?」といった疑問が湧いてくるかもしれません。これこそが **第2のパズル** です。
この第2のパズルには、数学の力で答えることができます。箱の中にきれいに収まっていることは,ちゃんと証明できます。しかもその証明は中学の数学レベルで理解できるエレガントで簡単なものです。さらに,この2種類の立体で遊んでいる中で,これらがタイリングなどの綺麗な性質を持った”特別な"多面体だということがとわかってきます。
どうぞ、このパズルを最後まで楽しんでください。
- セット内容:パズルピース×9、パズルケース(大)×1、パズルケース(小)×1、解説書
- 対象年齢:8歳以上
- 価格:¥2,750 税込
- 商品コード:IMCB001
開発ヒストリー
- 2021『イマジナリーキューブパズル 3H=6T』(普及版) イメージミッション木鏡社
(ピースはプラスチック製で、一辺3cmの立方体に入ります。) - 2012『イマジナリーキューブパズル 3H=6T』(パズル付き冊子) 京都大学総合博物館ミュゼップ(アクティブKEI) ※欠品中
(ピースは木製で、一辺4cmの立方体に入ります。)