フラクタルの影が面積をもつ方向

シェルピンスキー四面体，H-フラクタル，T-フラクタルの 3 個のフラクタルイマジナリーキューブは，光をあてる方向によって，正方形をはじめとする面積を持つ影をもつ場合と，面積が0の影をもつ場合がありました。どういう時に面積をもつ影ができるのでしょうか？

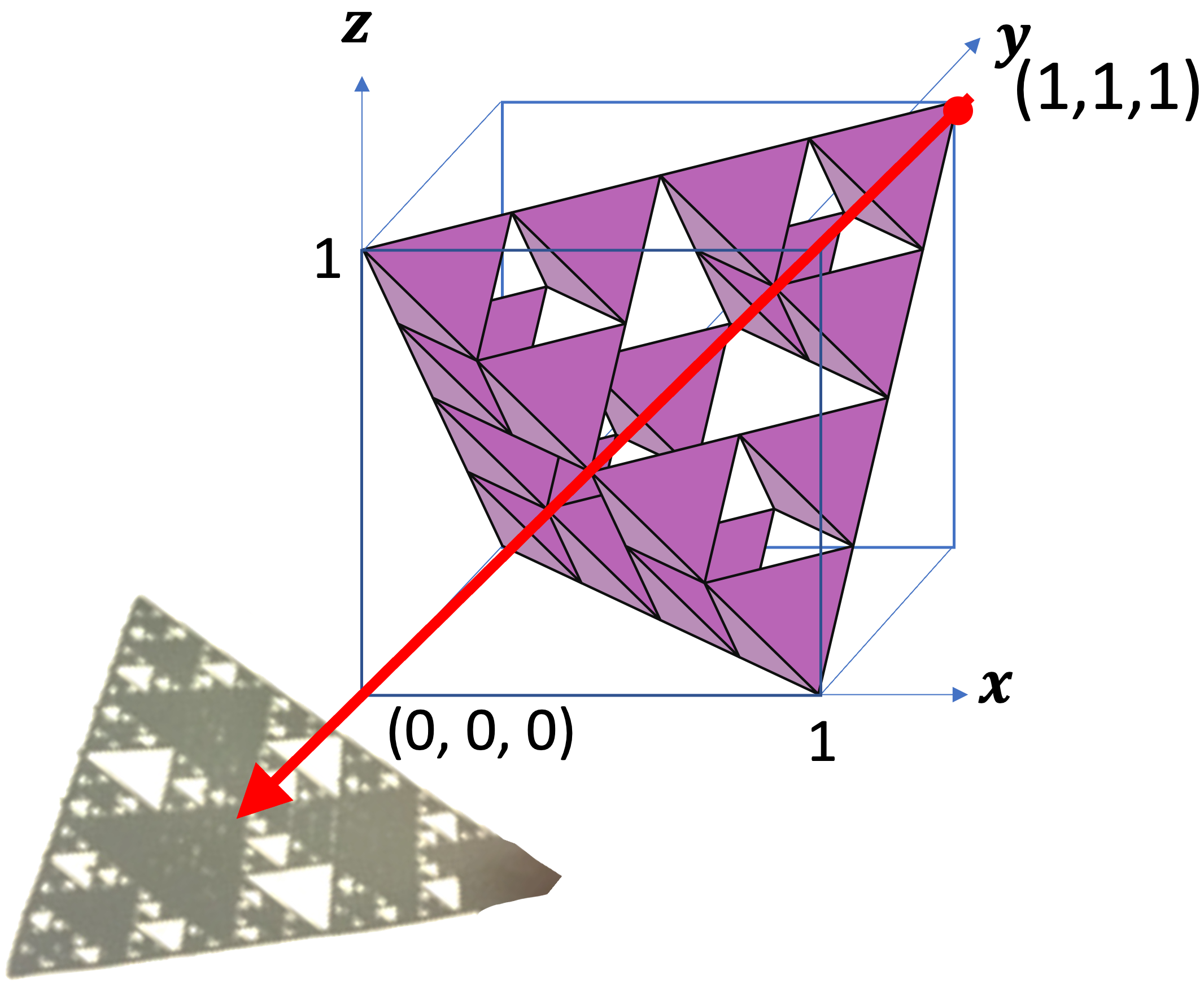
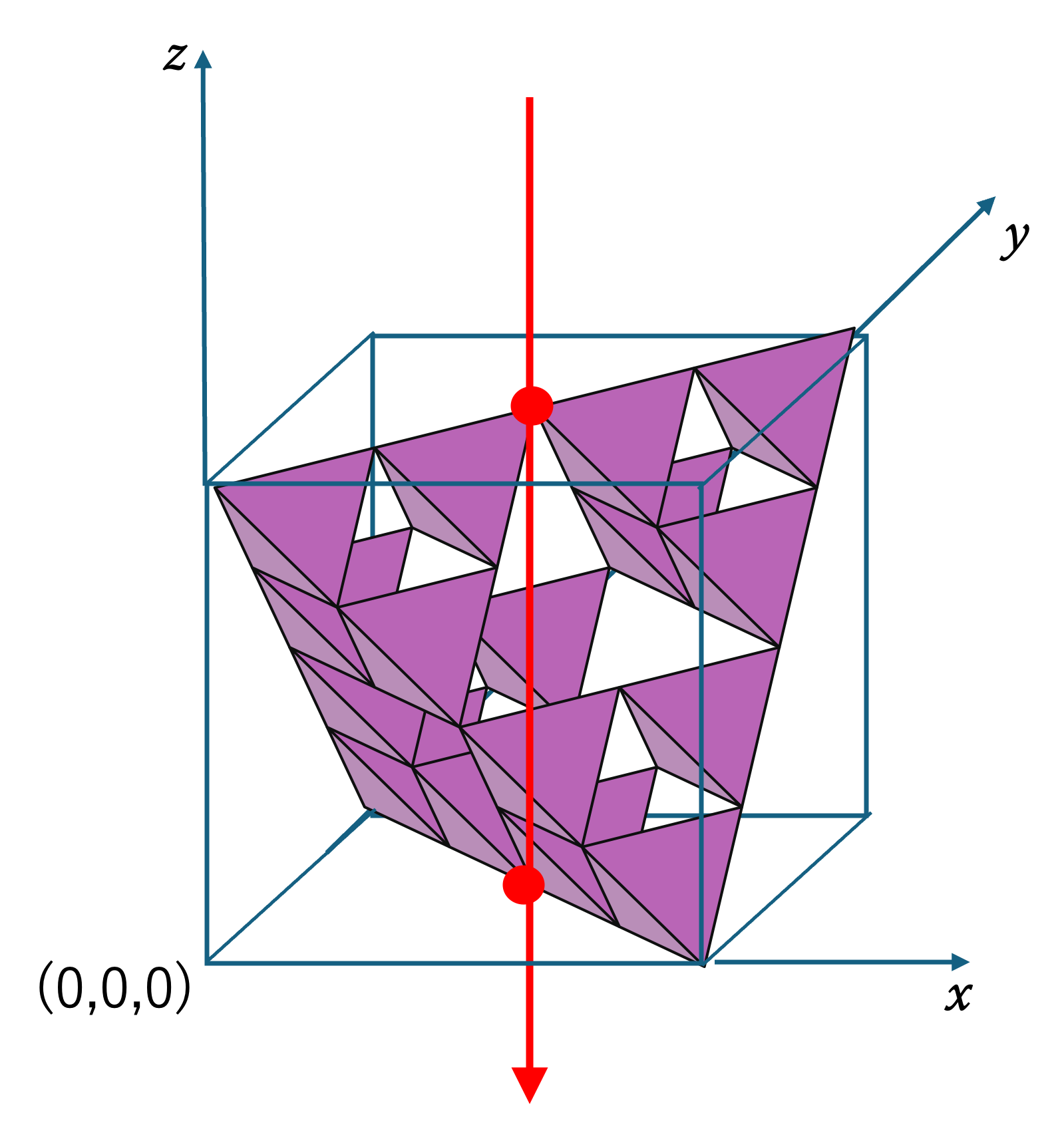
上図のように，これらのフラクタルを辺の長さが 1 の箱に入れた状態で考えましょう。そして，箱の左手前の頂点を原点にして，箱の3辺を x, y, z 軸とし， (a, b, c) という座標から原点に向けて光をあてて影を作っているとします。その時に，次のことが成り立ちます。

• まず，aと b, b と c, c と a のどれかの比が無理数の時には，影の面積は 0 になります。
• そうでない時，すなわち a, b, c の比が有理数の時には， a, b, c それぞれに何かを掛けても光の方向は変わらないので，a, b, c がすべて有理数と考えても大丈夫です。さらに，a, b, c の分母の最小公倍数をかけることにより，a, b, c が整数の場合だけを考えればいいです。さらに，最小公約数で割ることにより，a, b, c が互いに素(すなわち，公約数をもたない) 時だけを考えればいいです。a, b, c が互いに素な整数の時，次のことが言えます。
  • シェルピンスキー四面体の場合には，a, b, c の和が奇数となる方向から光をあてれば正の面積の影ができ，偶数なら面積が 0 の影ができます。
  • T-フラクタルの場合には，a, b, c の和が 3 の倍数でないなら正の面積をもち， 3 の倍数なら面積が 0 になります。
  • H-フラクタルの場合には，a, b, c の和が 3 の倍数でないか， a と b と -(a+b+c)/3 を 3 で割った余りが全て 1 か 全て 2 であるなら正の面積をもち，それ以外なら面積が 0 になります。少し計算をすると，前者の条件を満たす (a,b,c) の方向を x=y=z の軸の周りで 60 度回転すると，後者の条件を満たす方向になることがわかります。

H-フラクタルの場合に T-フラクタル の場合より光をあてて正方形になる方向がたくさんあるのは，H-フラクタルがダブルイマジナリーキューブであることと関係しています。

この結果は，これら3個のフラクタルをより一般化した Layered Fractal Imaginary Cube に対して証明がされています。詳細は， この論文 をご覧ください。

具体例

具体例でこのことを確認してみましょう。

上の絵と射影方向から，どんな影ができるか想像しながらご覧ください。

• (0,0,1)

  

  上の正方形の3個の絵は，座標軸方向，すなわち，(1,0,0), (0,1,0), (0,0,1) から射影して得られます。 1 + 0 + 0 = 1 は奇数でもあり3で割り切れない数でもあり，面積を持つための条件と合致しています。 　 それに加えて，H の場合は，(-1,2,2), (2,-1,2), (2,2,-1) からの射影でも正方形の影ができます。

• (1,1,1)

  

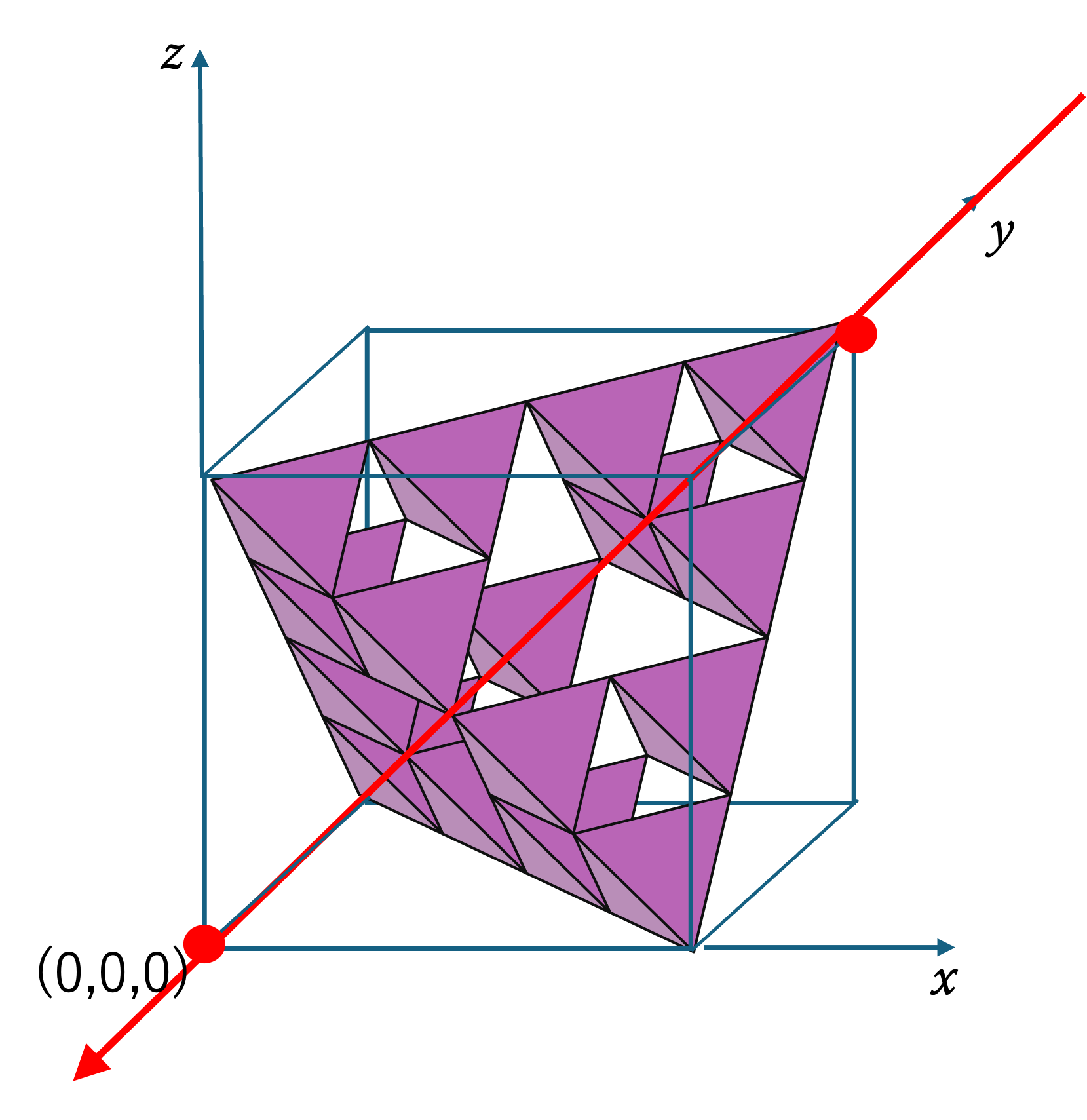
  これは，(1,1,1) からの射影像です。 シェルピンスキー四面体は 1 + 1 + 1 が奇数なので面積のある影ができ， H-フラクタルと T-フラクタルは 1+1+1 が3の倍数なので面積 0 の影ができます。

• (1,1,0)

  

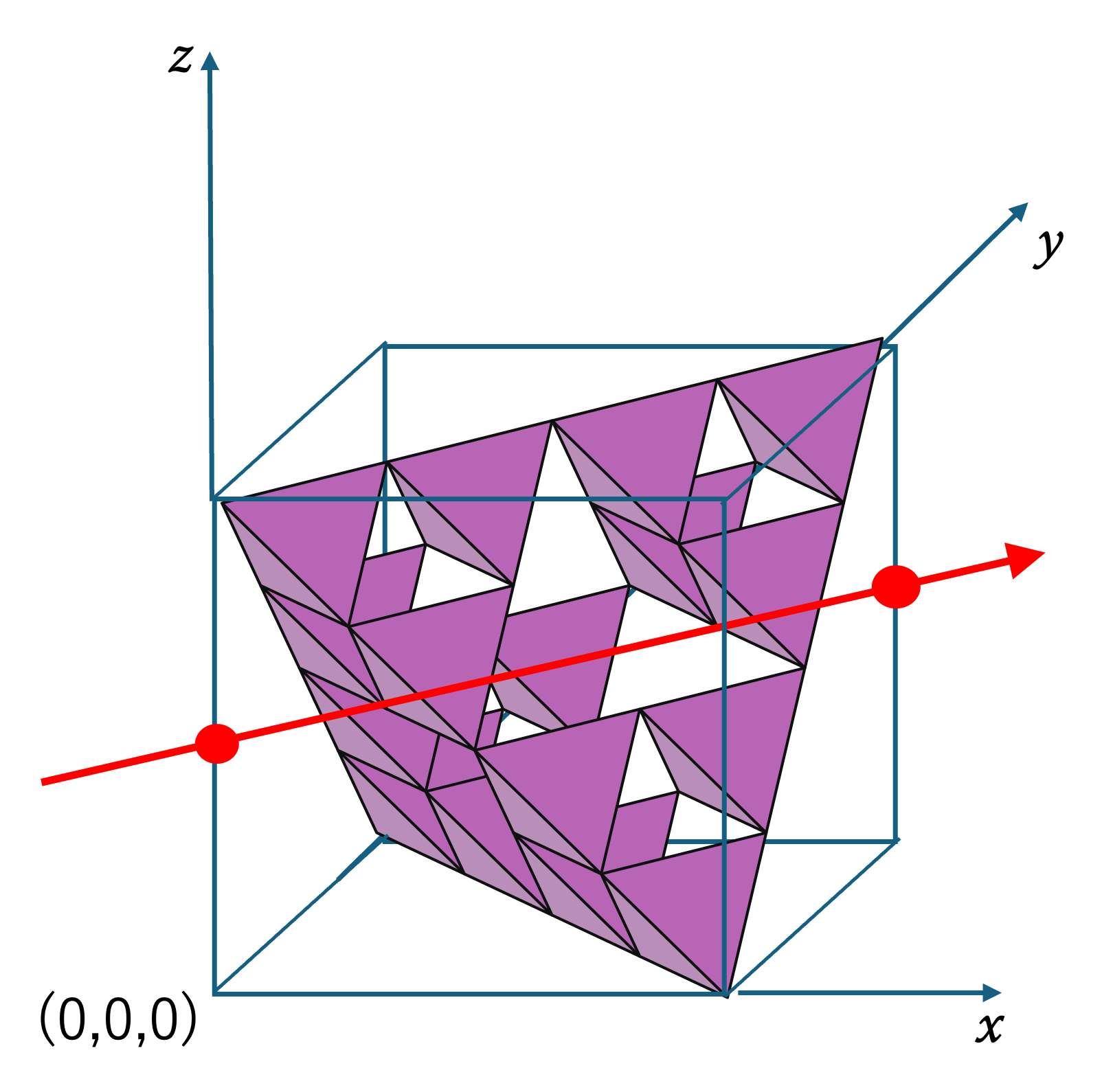
  これは，(1,10) (および，(0,1,1), (1,0,1))) 方向からの射影像です。1+1+0 = 2 は偶数ですが 3 の倍数ではないので，S については面積 0で, H と T については正の面積をもちます。 この H と同じ影は，(1,0,4) (および，(0,4,1), (4,1,0)) 方向からの射影でも得られます。

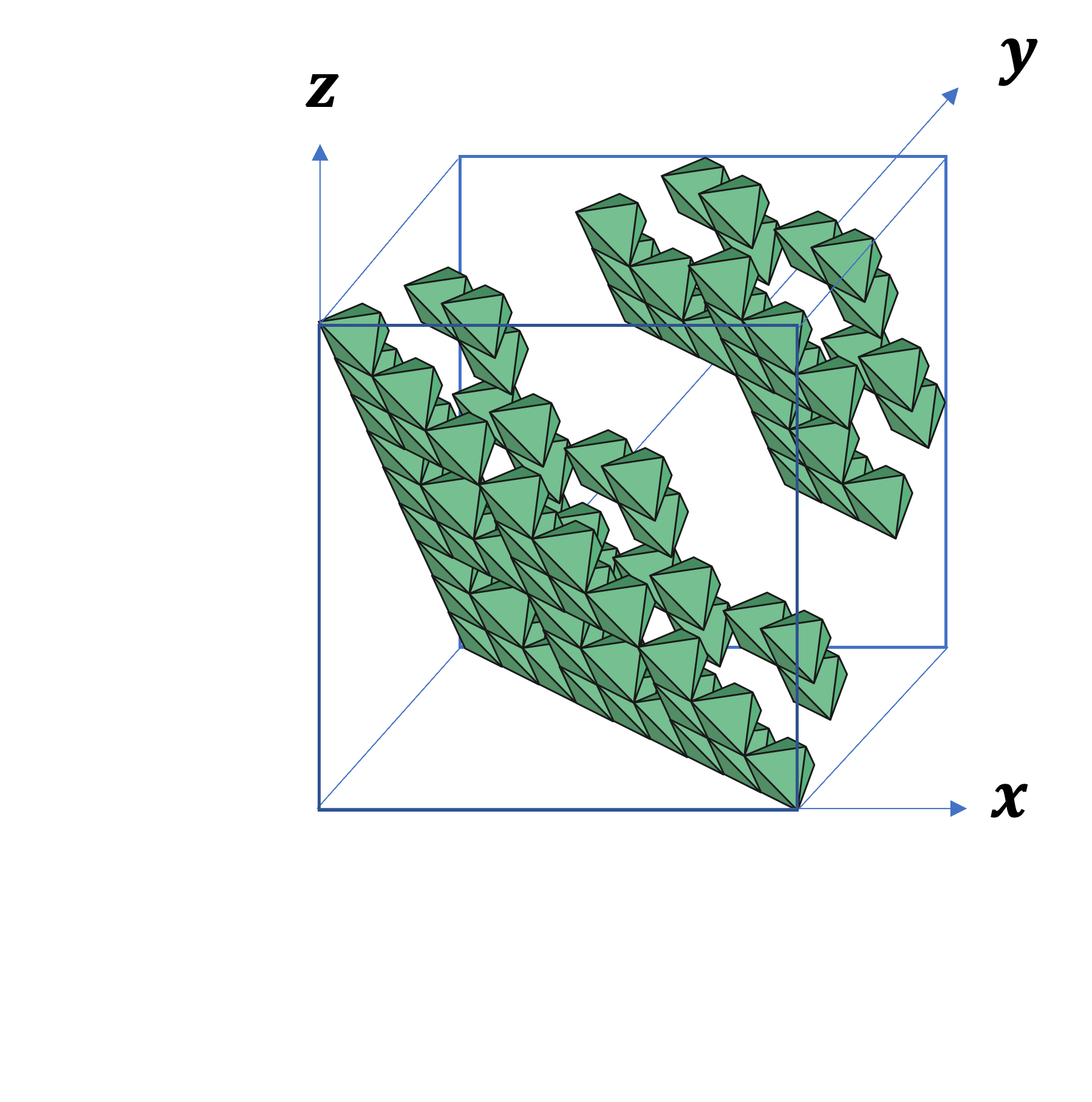
• (1,1,-1)

  

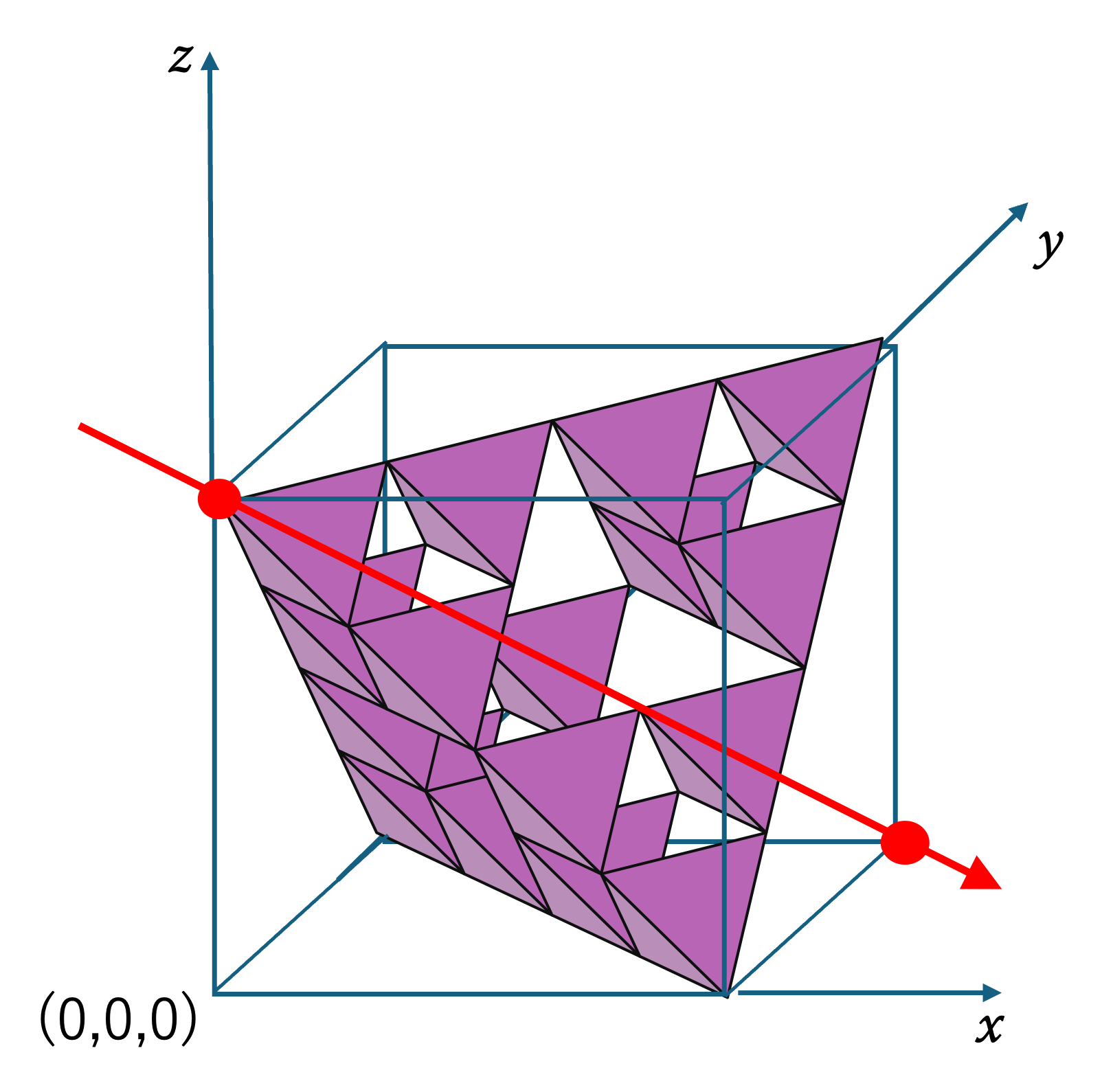
  これは，(1,1,-1) (および，(-1,1,1), (1,-1,1)) 方向からの射影像です。1+1+(-1) = 1 は2 の倍数でも3の倍数でもないので，どの影も面積があります。また，この H と同じ影は， (1,1,-5) (および，(-5,1,1), (1,-5,1)) からの射影でも得られます。

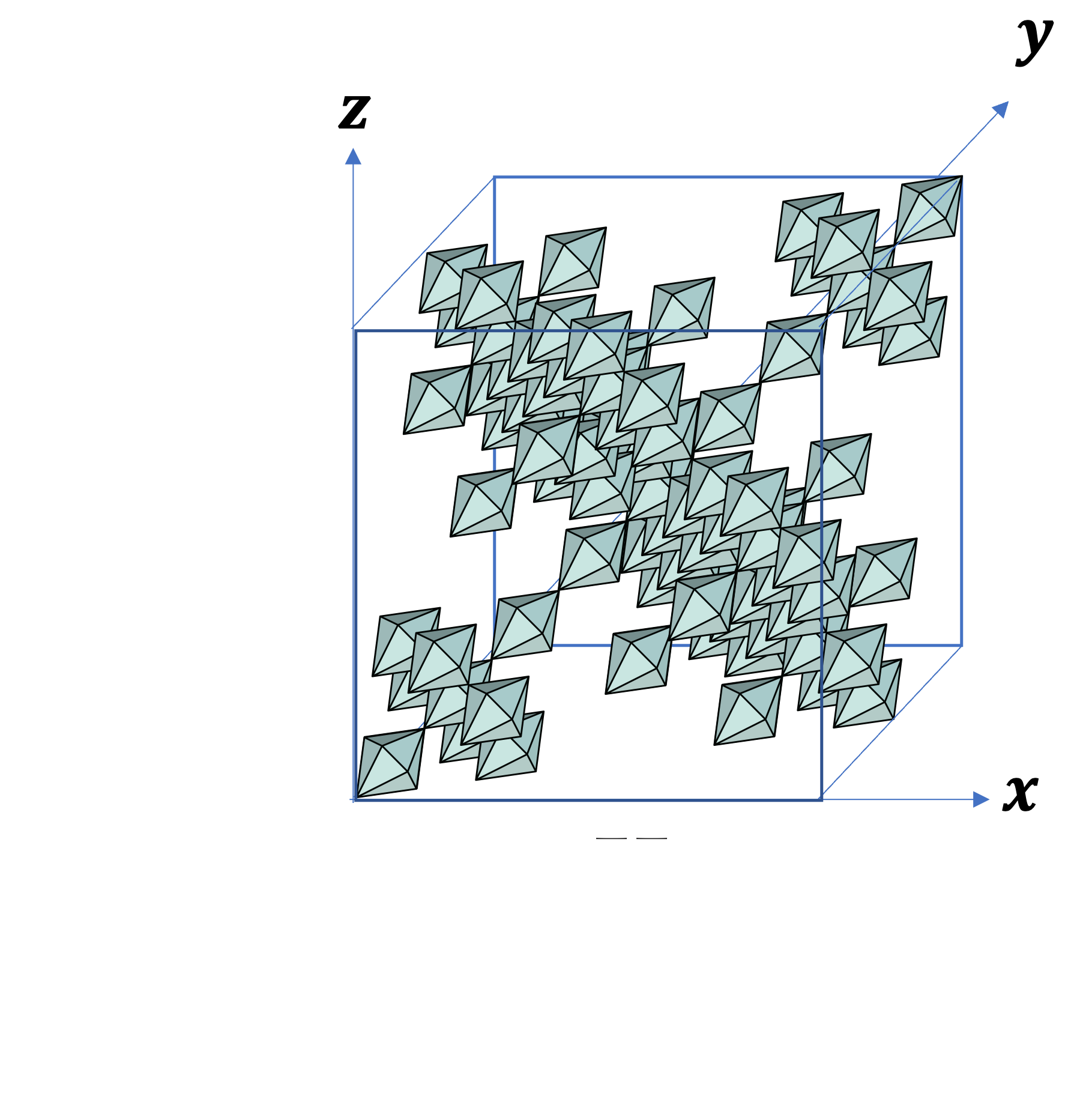
• (1,1,-2)

  

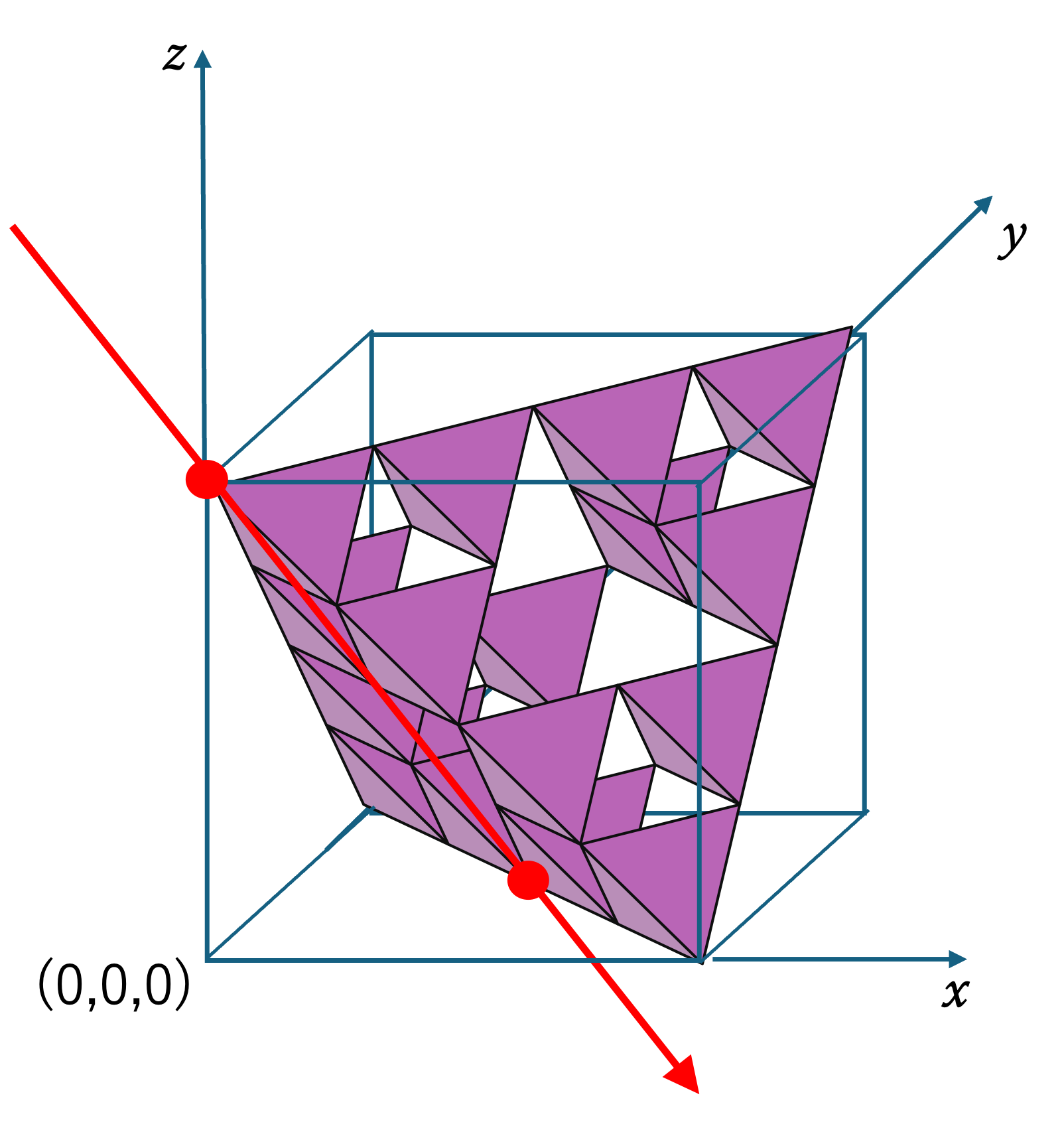
  最後に， これは (1,1,-2) (および (-2,1,1), (1,-2, 1)) 方向からの射影像です。1+1+(-2) = 0 は偶数でも3の倍数でもあるので，どの影も面積 0 です。