T-フラクタル
シェルピンスキー四面体は,フラクタルであるようなイマジナリーキューブでした。他にも,フラクタルイマジナリーキューブはあるでしょうか?そのことを調べている中で,その次に単純なフラクタルイマジナリーキューブが二つあることがわかりました。 それらは,パズルの立体である H と T を基本図形としたフラクタルです。
まず, そのうち T-フラクタルについて説明しましょう。
T は次のような立体でした。
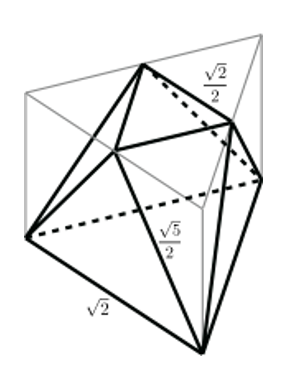
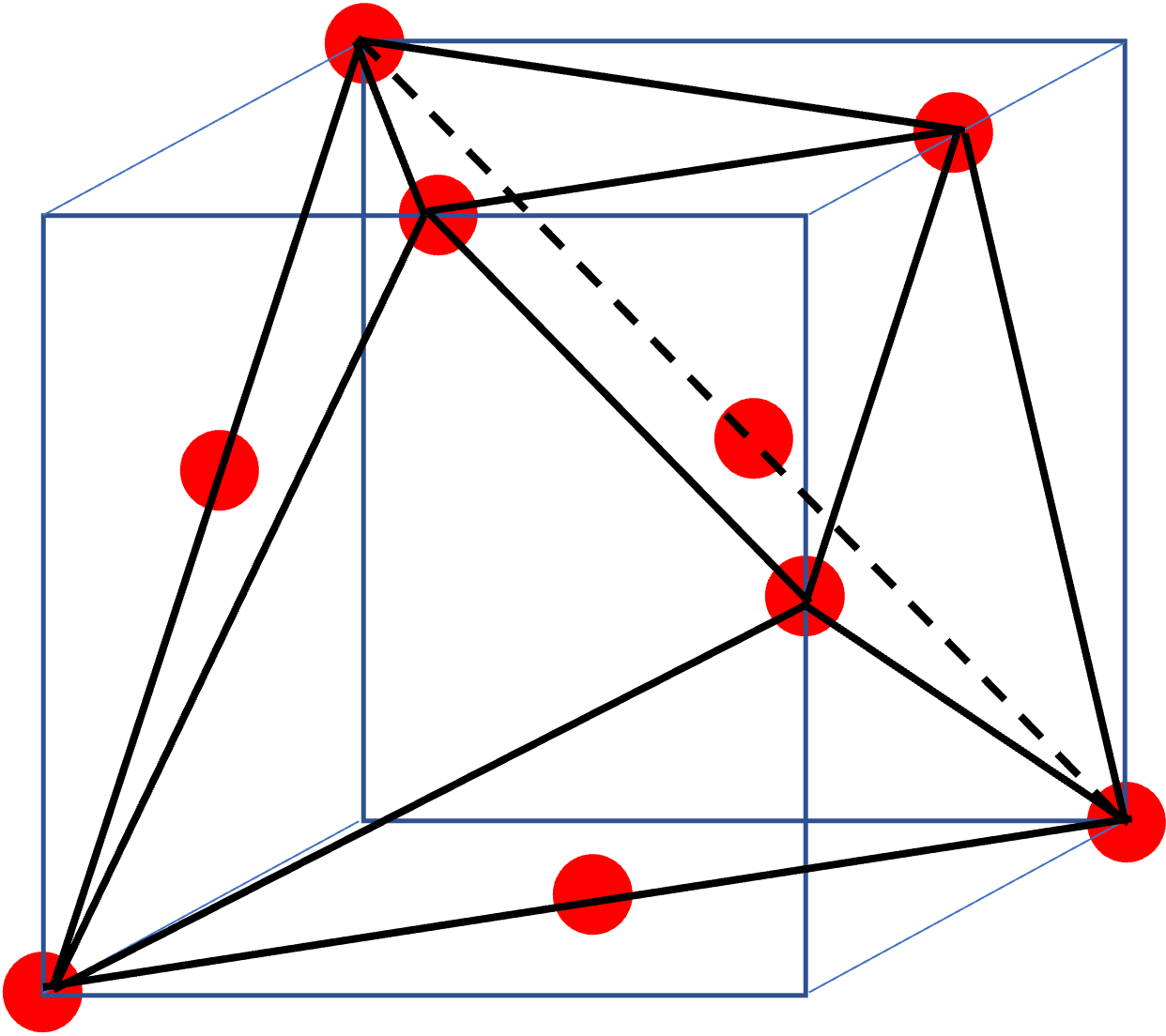
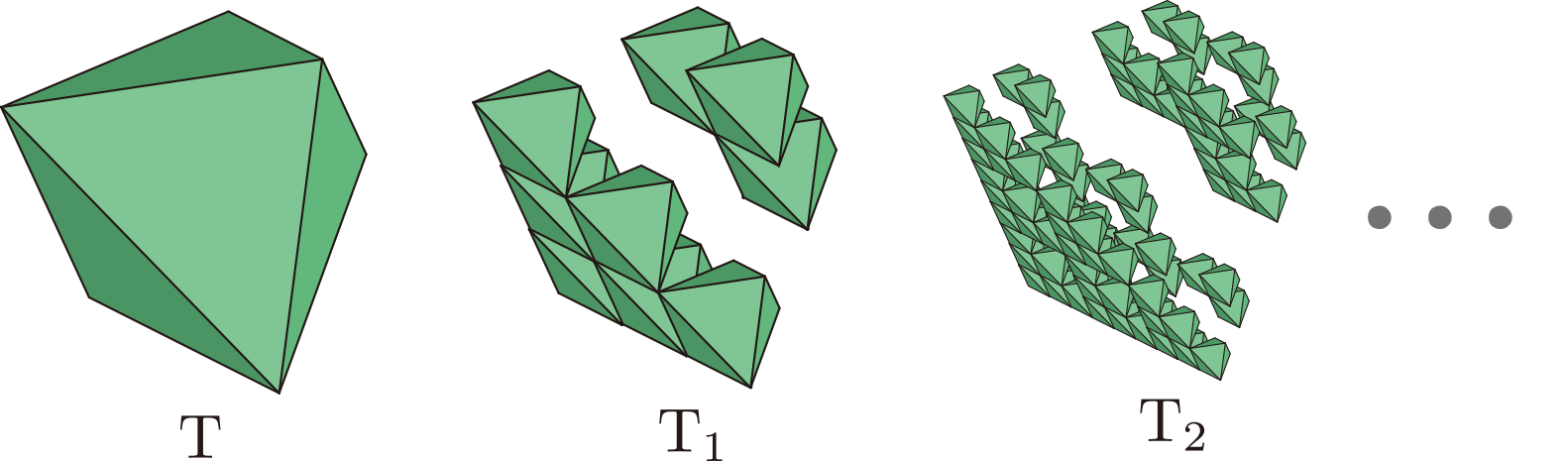
T-フラクタルも,自分の縮小像を集めてできた立体を作る操作を繰り返すことによりできています。上図の赤丸の9個の点(T の 6 個の頂点と底面の3 辺の中点) を中心として T を1/3 に縮小して合わせた立体 T1 を作ります。 次に,同じ操作を T1 に対して行い,立体 T2 を作ります。同じことを繰り返すと,立体が小さくなっていく列
T, T1, T2, ... ができます。
T-フラクタルはイマジナリーキューブ
下の写真は,立方体の箱に入れた T, T1, T2, T3,... を3Dプリントで作成したものです。 これらの立体は,全てイマジナリーキューブです。




そして,その極限の T-フラクタルもイマジナリーキューブです。

T-フラクタルの影
T-フラクタルの影も自己相似図形です。T-フラクタルの近似模型を,光のもとで回転させると,下図のように影が連続に変化していきます。ほとんどの影は,近似立体ではなく完全な T-フラクタルを考えた時には面積が 0 になりますが,正方形をはじめ,上の3個の写真のように面積を持った影も現れます。







どういう方向から光をあてると,面積をもつ影ができるかについては,「フラクタルの影」の章で説明します。